Datenanalyse in SPSS kurz erklärt

Datenanalyse SPSS: Statistik mit SPSS kann kompliziert sein, doch hier erfährst Du das allgemeine Vorgehen bei einer Datenanalyse mit SPSS. Nachdem Daten Importieren in SPSS oder Eintippen folgt die Überprüfung der Daten. Sind sie vollständig? Sind sie gültig? Wie sind die Daten verteilt? Die Auswertung Deiner Daten lässt sich dabei grob in drei Bereiche einteilen: die beschreibende (deskriptive), die erkundende (explorative) und die schließende (inferenzstatistische) Analyse. In einem praktischen Beispiel demonstrieren wir das allgemeine Vorgehen. Weiterhin wird das Ergebnis eines Hypothesentests näher erläutert.

Datenanalyse SPSS: Allgemeines zur deskriptiven Statistik

Die deskriptive Statistik eignet sich für die ersten Schritte Deiner Analyse. Denn sie kann Dir dabei helfen, Fehler in den Daten zu finden. In SPSS kannst Du die beschreibende Statistik auch mit passenden Diagrammen ergänzen. Somit erhältst Du beispielsweise eine Idee deiner SPSS Datenverteilung. Du bekommst dadurch auch eine erste Vorstellung davon, ob bestimmte Voraussetzungen für die Durchführung der nachfolgenden statistischen Verfahren erfüllt sind.

Laden der Beispieldatei

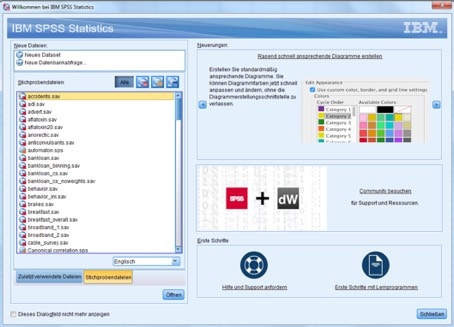
SPSS liefert mit der Installation einige Beispieldatensätze. Öffne dazu im Begrüßungsbildschirm die Datei demo.sav. Sie enthält Daten eines Telefonanbieters.

Abbildung 1: Begrüßungsbildschirm mit Beispielen

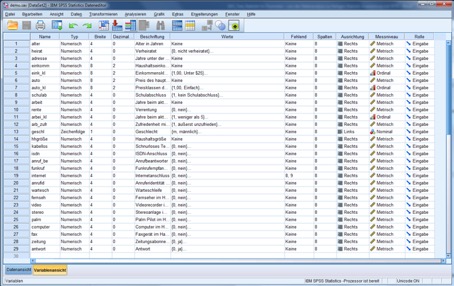
Du kannst in SPSS zwischen der Datenansicht und der Variablenansicht wechseln. Die Datenansicht enthält in der Regel die Fälle und die Datenpunkte. Wohingegen die Variablenansicht die ausführliche Beschreibung der Variablen enthält. Beispielsweise kannst du hier unter Berücksichtigung der SPSS Syntax den Namen der Variablen und eine genauere Beschreibung einfügen.

Abbildung 2: Variablenansicht in SPSS

Nachdem Du den Datensatz geprüft hast, fertigst Du die deskriptive Statistik an.

Mittelwert, Modus, Median, Standardabweichung und Varianz mit SPSS berechnen

Wichtige Kennzahlen der beschreibenden Statistik sind vor allem Median, Modus sowie das arithmetische Mittel. Aber auch Parameter der Streuung wie die Standardabweichung und Varianz. Beispielsweise verwendest Du die Variablen „alter“, „heirat“, „einkomm“ und „internet“.

Erst einmal wechselst Du in die Datenansicht. Dabei erkennst Du, dass das Alter ganzzahlig und nicht als Kategorie abgefragt wurde. Hier ist das Messniveau für „alter“ als metrisch hinterlegt.

Die Variable „heirat“ ist als numerischer Datentyp angegeben. Darüber hinaus ist unter der Spalte “Werte” der Datenwert eingetragen.  0 = bedeutet „nicht verheiratet“ und 1  =„verheiratet“. Die Variable „einkomm“ beinhaltet gemäß der eingetragenen Beschriftung das “Haushaltseinkommen in Tausend”. Wenn du hier Schwierigkeiten bei der Zuordnung hast, empfiehlt sich die Statistik-Beratung.

Deskriptive Statistik – Datenanalyse mit SPSS

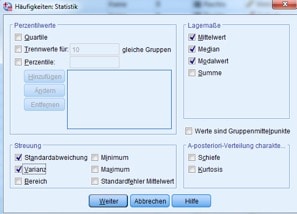
Jetzt erklären wir Dir, wie Du eine deskriptive Statistik Datenanalyse mit SPSS umsetzt. Zum Anfertigen der deskriptiven Statistik wähle in SPSS „Analysieren“, dann „Deskriptive Statistiken“ und „Häufigkeiten“. Anschließend ziehst Du die Variablen in das rechte Feld. Nimm die Auswahl wie in Abbildung 3 vor. Schließlich bestätigst Du die Eingabe mit der Schaltfläche „Weiter“.

Abbildung 3: Einstellungen für die deskriptive Statistik

Nun erscheint im Ergebnis-Fenster der SPSS Software die Auswertung. Die Spalten stellen hier die ausgewerteten Variablen dar. Allerdings ist die Berechnung des Medians oder des arithmetischen Mittels nicht für alle Variablen gleich sinnvoll. Das arithmetische Mittel verwendest du bei metrisch skalierten Variablen. Wohingegen der Median mindestens Ordinalskalen Niveau voraussetzt.

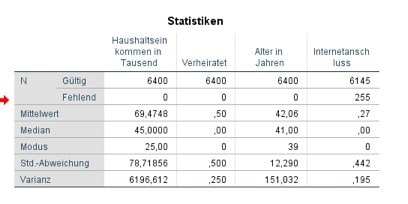
Der Median teilt die Daten der Variable in zwei Hälften. Denn er ist quasi der Wert in der Mitte. Das arithmetische Mittel der Variable „Haushaltseinkommen in Tausend“ liegt hier bei M=69,47. Allerdings liegt der Median bei der gleichen Variable bei MD= 45. Die Standardabweichung ist die mittlere Abweichung der Werte von ihrem Mittelwert. Des Weiteren bildet die Varianz die mittlere quadratische Abweichung.

Abbildung 4: Datenausgabe der Statistik in SPSS

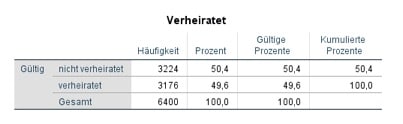
Der Modus ist der am häufigsten vorkommende Wert bei einer Variable. 39 Jahre ist in unserem Beispiel in der Variable „Alter in Jahren“ also die häufigste Nennung. Das arithmetische Mittel ist bei nominalskalierten Daten eigentlich nicht verwendbar. Allerdings erkennst Du damit in unserem Fall, dass etwa gleich viele befragte Personen verheiratet sind (M=0,5). Etwas genauer ist hier die Ausgabe der Tabelle der Häufigkeiten der Variable „Verheiratet“.

Abbildung 5: Häufigkeitstabelle der nominal skalierten Variablen „Verheiratet“

Kennzahlen nach Gruppen in der deskriptiven Statistik

Nun hast Du einige Kennzahlen einzelner Variablen berechnet. Des Weiteren möchten wir die beschreibende Statistik getrennt nach Gruppen bilden.

Wähle dazu „Daten“ und „Datei aufteilen“. Anschließend legst Du eine kategoriale Variabel als Teilungsvariable fest. Nun kannst Du die Analyse, genauso wie vorher beschrieben, abermals durchführen. Alternativ kannst Du natürlich entspannt den Datenanalyse Service in Anspruch. Nachdem Du die Analyse durchgeführt hast, erhältst Du die Kennzahlen pro Gruppe. Der Median und das arithmetische Mittel sind in der Stichprobe der nicht verheirateten und der verheirateten Stichprobe fast gleich. Zudem ist erkennbar, dass in beiden Gruppen die Verteilung wegen des fast identischen Medians und Mittelwerts annähernd zentriert ist.

Verheiratet			Haushaltseinkommen in Tausend	Verheiratet	Alter in Jahren	Internetanschluss
nicht verheiratet	N	Gültig	3224	3224	3224	3098
		Fehlend	0	0	0	126
		Mittelwert	69,2723	,00	42,02	,27
		Median	44,5000	,00	41,00	,00
		Modus	25,00	0	40	0
		Std.-Abweichung	78,32925	,000	12,326	,444
		Varianz	6135,471	,000	151,934	,197
verheiratet	N	Gültig	3176	3176	3176	3047
		Fehlend	0	0	0	129
		Mittelwert	69,6804	1,00	42,10	,26
		Median	45,0000	1,00	41,00	,00
		Modus	22,00	1	39	0
		Std.-Abweichung	79,12361	,000	12,254	,440
		Varianz	6260,546	,000	150,162	,194

Abbildung 6: Deskriptive Statistik getrennt angegeben für eine kategoriale Variable.

Dies führt uns auch schon zum nächsten Schritt: statistische Tests. Zunächst einmal der Hypothesen- Test. Vergesse nicht den Split-Befehl in SPSS für die folgende Analyse zu löschen.

Prinzip des Hypothesentests für eine Datenanalyse mit SPSS

Beim statistischen Testen einer Hypothese gibst Du ein Hypothesenpaar an (vgl. Field 2017). Dieses prüfst Du dann mittels Berechnung auf Gültigkeit. Die Nullhypothese ist häufig so formuliert, dass kein Effekt vorliegt und beispielsweise eine Korrelation in SPPS nicht daraus hervorgeht. Die Nullhypothese lautet bei einem ungerichteten t-Test für abhängige Stichproben: „Die Mittelwerte beider Gruppen sind gleich“. Die Alternativhypothese enthält den Effekt. Beim t-Test heißt sie: „Die beiden Gruppen unterscheiden sich“. Nun vergleichst Du den errechneten Wert mit einem Schwellenwert. Die Nullhypothese kannst Du verwerfen, wenn der errechnete Wert unter dem Vergleichswert liegt. Dann gilt die Alternativhypothese.

Der t-Test – Beispiel für Datenanalyse mit SPSS

In einem einfachen Beispiel wollen wir das Prinzip bei einem t-Test für eine Datenanalyse in SPSS ansehen. Beispielsweise möchtest Du testen, ob sich verheirate und unverheiratete Personen hinsichtlich ihres Alters unterscheiden.

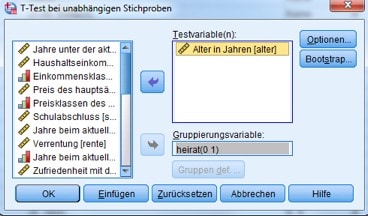
Wähle „Analysieren“, dann „Mittelwerte vergleichen“ und „T-Test bei unabhängigen Stichproben“.

Abbildung 7: T-Test bei unabhängigen Stichproben

Für das Gelingen des t-Tests sollte die abhängige Variable metrisch vorliegen. Die Verteilungen der beiden Gruppen sollten in der abhängigen Variable annähernd normalverteilt sein. Außerdem solltest Du prüfen, ob die Varianzen in den Gruppen annähernd gleich sind. Diese kannst Du mit dem Levene-Test testen. Schließlich kannst du das Ergebnis direkt in der Ausgabe des t-Tests ablesen (zur Prüfung der Voraussetzungen kannst Du dich z.B. auf der Website eines Professors der University of Sussex genauer informieren).

Levene-Test mit SPSS

Der Levene-Test prüft die Nullhypothese: „Die Varianzen der Gruppen sind gleich“. Der Signifikanztest liefert das Ergebnis p=0,888. Erst einmal vergleichst Du den p-Wert mit einem Referenzwert. In der Regel kannst Du 0,05 als Referenz nutzen. Wenn der errechnete Wert über diesem liegt, kannst Du somit die Nullhypothese nicht verwerfen. In diesem Fall können die Varianzen als gleich angenommen werden.

Interpretation des t-Tests

Nun bleibst Du in der ersten Zeile des SPSS-Outputs. Die Nullhypothese des t-Tests lautet: „Die beiden Mittelwerte der Stichproben sind gleich“. In der Spalte „Sig (2-Seitig)“ liest Du nun den p-Wert des t-Tests ab. Hier ist der Wert ebenfalls über dem 0,05er Schwellenwert. Auch hier kann die Nullhypothese nicht abgelehnt werden. Im Zweifelsfall kann der Statistik-Service mehr Klarheit schaffen.

Abbildung 8: Tabelle mit Ergebnissen des T-Tests in SPSS

Wäre der p-Wert unterhalb der 0,05 Grenze, könntest Du die Nullhypothese verwerfen. Dann gilt die Alternativhypothese. In jenem Fall bestünde also ein Unterschied zwischen den beiden Stichproben hinsichtlich des Alters.

In diesem Beispiel wird die Verzahnung von deskriptiver und schließender Statistik deutlich. Nutze also die modernen Möglichkeiten der Datenanalyse mit SPSS, um die Qualität Deiner Auswertung zu steigern. Überdies solltest du unbedingt das SPSS Python Programmieren in Betracht ziehen. Die deskriptive Statistik hilft Dir beim Überprüfen von Voraussetzungen der weiteren Analyse in SPSS. Meist schließen sich hier Verfahren zur Testung von Hypothesen an. Mit deren Hilfe kannst Du Deine Forschungsfragen beantworten.

Literatur

Field, Andy (2017): Discovering Statistics Using IBM SPSS Statistics, 5. Auflage London.

Wooldridge, Jeffery (2013): Introductory Econometrics: A modern approach, 5. Auflage Mason (OH).