Statistische Tests sind mächtige Werkzeuge in der Kommunikation von statistischen Aussagen. Es ist ein großer Unterschied ob Du lediglich Zahlen oder Grafiken vorlegst oder diese auch mit statistischen Methoden signifikant absichern kannst. Zwei Beispiele sollen diesen Ansatz verdeutlichen.
Was sind statistische Tests?
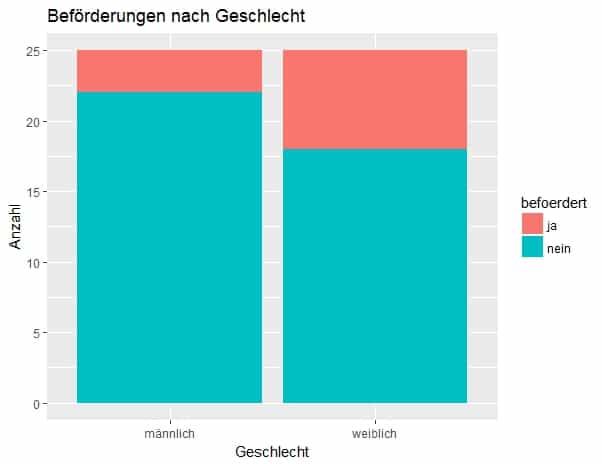
Im ersten Beispiel betrachten wir eine Stichprobe aus einem fiktiven Unternehmen. In der Personalabteilung soll untersucht werden, ob ein Geschlecht bei Beförderungen bevorzugt wird. Das Ergebnis bei der Betrachtung von 50 Mitarbeitern sieht folgendermaßen aus.
Abb. 1: Grafik erstellt mit der Statistiksoftware R und dem Package ggplot2
Du kannst sehen, dass in dieser Stichprobe mehr Frauen als Männer befördert wurden.
Ein zweites Beispiel für statistische Tests, stammt aus der Marketingabteilung in einem Unternehmen. Um zu überprüfen, ob eine Werbemaßnahme wirksam war, werden stichprobenartig Verkaufszahlen von 25 Verkaufsstellen vergleichbarer Größe eingeholt. Aus der Vorperiode sind durchschnittliche Verkaufszahlen von 50.000 € bekannt. Bei der Stichprobe liegt der Durchschnitt bei 51.000 € mit einer geschätzten (errechneten) Standardabweichung von 2.500 €. Wie und mit welchem statischen Test sichert das Team ab, dass signifikant mehr Umsatz erzielt wurde?
Wie Du siehst, sind die beiden Fragestellungen von unterschiedlicher Natur. Einmal wollen wir die (Un-)Abhängigkeit zweier Variablen überprüfen (Geschlecht und Beförderung). Das andere Beispiel sucht nach Rückschlüssen von der Stichprobe auf den wahren Mittelwert der Verkaufszahlen.
Wenn statistische Tests zum ersten Mal in der Uni (oder andernorts) besprochen werden, neigen Studierende dazu, die verschiedenen Tests losgelöst voneinander zu betrachten. Dies ist ein ganz normaler Impuls, da Fragestellungen und Rechnungen sehr unterschiedlich erscheinen. Bei genauerer Betrachtung lässt sich jedoch ein gemeinsamer Ablauf Tests erkennen. Dieser gemeinsame Ablauf, soll Dir in diesem Text vermittelt werden. Wenn Du Dir statistische Tests als Werkzeuge in einem Werkzeugkasten vorstellst, handelt es sich nicht um grundlegend verschiedene Werkzeuge, wie Säge, Hammer und Schraubendreher, sondern vielmehr um verschiedene Varianten eines Werkzeugs, wie Laubsäge, Metallsäge und Fuchsschwanz. Du musst also wissen, wann Du statistische Tests brauchst und welchen, aber die Anwendung aller Tests ist sehr ähnlich. Dabei kann die übrigens auch ein Datenanalyse-Service helfen.
Das Hypothesenpaar für statistische Tests
Bevor Du irgendetwas rechnest, solltest Du Dir die Frage stellen, was Du überhaupt wissen möchtest. Hierzu stellst Du zwei Hypothesen auf. Die erste Hypothese wird Nullhypothese (H0) genannt und soll durch statistische Tests widerlegt (verworfen) werden. Sollte dies geschehen, bestätigst du damit die Alternativhypothese (H1). Somit formulierst du die Hypothesen so, dass die Alternativhypothese die zu bestätigende Aussage enthält. Hypothesentests in Stata sind beispielsweise sehr beliebt.
Beispiel 1:
H0: Die beiden Merkmale sind unabhängig vs.
H1: Die beiden Merkmale sind nicht unabhängig
Beispiel 2:
H0: Die neuen Verkaufszahlen sind kleiner gleich die Alten vs.
H1: Die neuen Verkaufszahlen sind größer als die Alten
Prüfgröße für statistische Tests berechnen
Bevor Du weiterliest, solltest du die folgenden Fragen einigermaßen beantworten können.
- Was ist eine Verteilung?
- Wie sieht eine Dichtefunktion aus?
- Was bedeutet die Fläche unter einer Dichtefunktion?
Falls Du diese Fragen grob beantworten konntest, lies weiter. Falls Du Dir in Teilen unsicher warst, solltest Du kurz die Grundlagen auffrischen (siehe auch die Hinweise der Fernuni Hagen).
In der Statistik nehmen wir an, dass Zufallsvariablen bestimmten Verteilungen folgen. Dies machen wir uns für die Bearbeitung unserer Fragestellung zu nutze. Du weißt also, was eine Verteilung ist und kannst anhand von Flächen in den dazugehörigen Dichtefunktionen Wahrscheinlichkeiten bestimmen.
Die Prüfgröße wird berechnet, da wir aufgrund der Verteilungsannahmen davon ausgehen, dass wir die Verteilung dieser Prüfgröße kennen. Dieser Schritt wirkt zunächst am kompliziertesten, da es je nach Test verschiedene Formeln zur Berechnung der Prüfgröße gibt und diese unterschiedlich verteilt sind. Wenn du jedoch die Grundrechenarten beherrschst und weißt, was ein Summenzeichen bedeutet, ist die Berechnung der Prüfgröße nur eine Sache der Übung. Für unsere Beispiele verzichten wir auf die Rechnung und schauen uns nur die fertige Prüfgröße und die passende Verteilung an.
Beispiel 1: Chi-Quadrat-Unabhängigkeitstest (nach Pearson)
Prüfgröße = 1.1
Verteilung = Chi² mit einem Freiheitsgrad. (X²(1))
Beispiel 2: T-Test
Prüfgröße = 2
Verteilung = Student-t Verteilung mit n – 1 = 24 Freiheitsgraden.
Ablehnungsbereich
Im dritten Abschnitt geht es um die Einordnung der Prüfgröße für statistische Tests. Hier gibt es zwei Möglichkeiten, welche beide valide Mittel sind, um eine Testentscheidung herbeizuführen. In diesem Abschnitt sehen wir uns den Ablehnungsbereich an und im nächsten Abschnitt den P-Wert.
Der Ablehnungsbereich oder Ablehnbereich, bezeichnet das oder die Intervalle in einer Verteilung, in der die Nullhypothese verworfen wird, falls die Prüfgröße im Ablehnungsbereich liegt. Dies klingt zunächst etwas kompliziert, ist aber ganz einfach. Wir sagen beispielsweise, die Prüfgröße ist standardnormal verteilt. Somit ist es wahrscheinlicher einen Wert nahe null zu erhalten, als einen Wert größer oder kleiner Null.
Abb. 2: Dichtefunktion einer Standardnormalverteilung
Der Trick ist nun, dass die Prüfgröße für statistische Tests unter Annahme der Nullhypothese berechnet wird. Somit wird es unwahrscheinlicher, dass die Nullhypothese zutrifft, wenn sich die Prüfgröße von null entfernt. Die Ablehnungsbereiche bilden wir demnach an den Rändern der Verteilung. Die Größe der Ablehnbereiche wird über unsere gewünschte Sicherheit gesteuert. Für diese Beispiele wird ein Signifikanzniveau von 0.05 angenommen. Die Intervallgrenzen der Ablehnbereiche können aus den Tabellen der passenden Verteilung entnommen werden.
Beispiel 1:
Die Prüfgröße ist Chi-Quadrat verteilt mit einem Freiheitsgrad. Dieser, und viele andere, statistische Tests sind rechtsseitig. Dies bedeutet, dass der Ablehnbereich auf der rechten Seite der Verteilung liegt. In Abhängigkeit von Test und Hypothese gibt es zusätzlich linksseitige und zweiseitige Tests.
Abb. 3: Statistische Tests: Chi-Quadrat-Verteilung mit einem Freiheitsgrad
Beispiel 2:
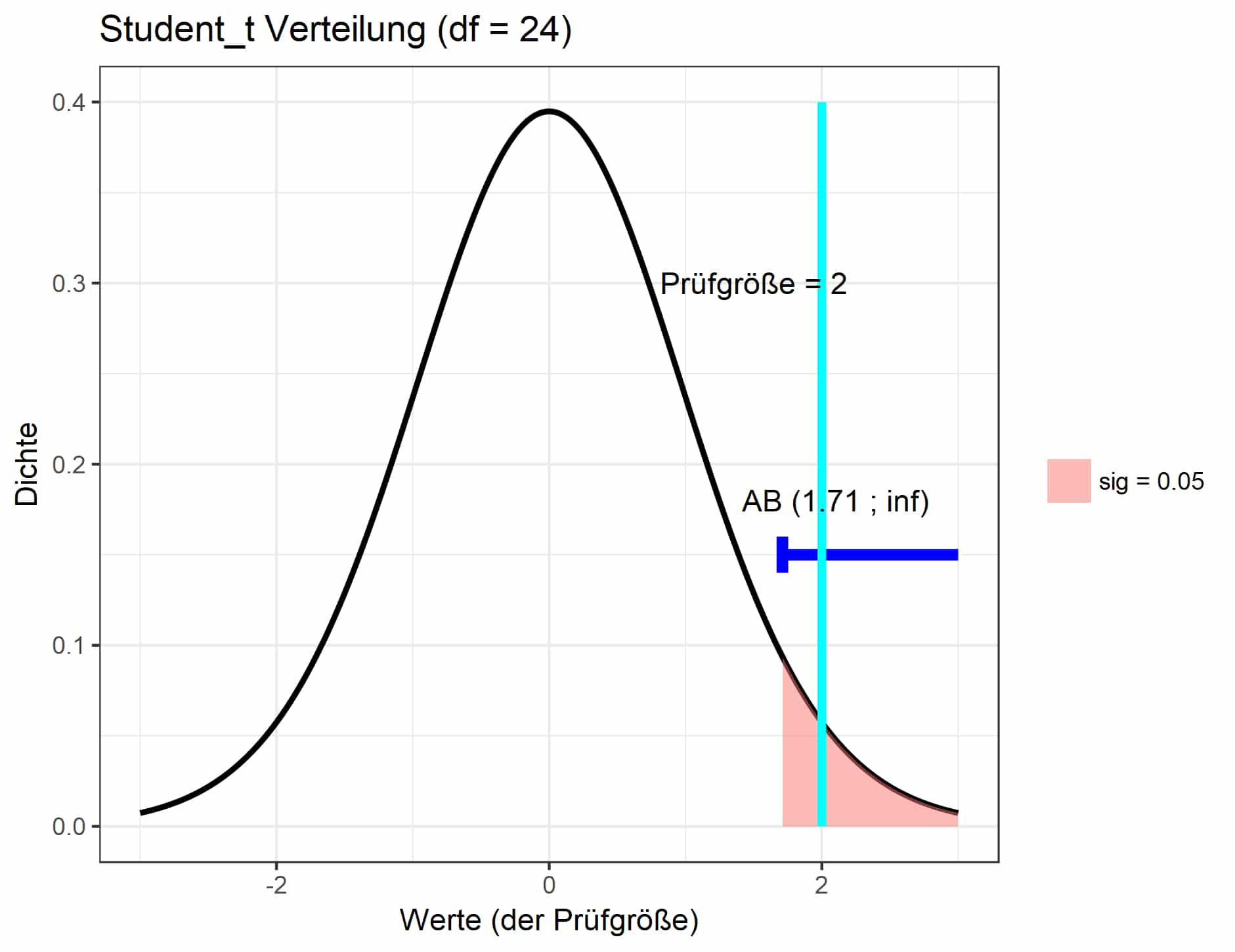
Die Prüfgröße ist t verteilt mit n-1 = 24 Freiheitsgraden.
Abb. 4: T-Verteilung mit 24 Freiheitsgraden
P-Wert
Der P-Wert ist eines der am häufigsten missverstandenen Konzepte in der Statistik. Die formale Definition lautet: Der P-Wert ist die Wahrscheinlichkeit, unter der Nullhypothese einen mindestens so extremen Wert für die Prüfgröße zu erhalten, wie den beobachteten (Zucchini 2009, 273). Grafisch lässt sich das Konzept einfacher nachvollziehen. In Abbildung 4 kannst du erkennen, dass links von der Prüfgröße noch ein bisschen Platz ist, bis der Ablehnbereich beginnt. Dieser Platz ist eigentlich „verschenkt“, da sich die Testentscheidung für statistische Tests nicht ändert, solange die Prüfgröße innerhalb des Ablehnbereichs liegt. Der P-Wert gibt nun dieses kleinstmögliche Signifikanzniveau an, bei dem die Nullhypothese noch verworfen werden kann. Wenn du hier Probleme hast, kann dir auch eine Statistik Beratung behilflich sein.
Beispiel 1:
Abb. 5: P-Wert im ersten Beispiel (rot).
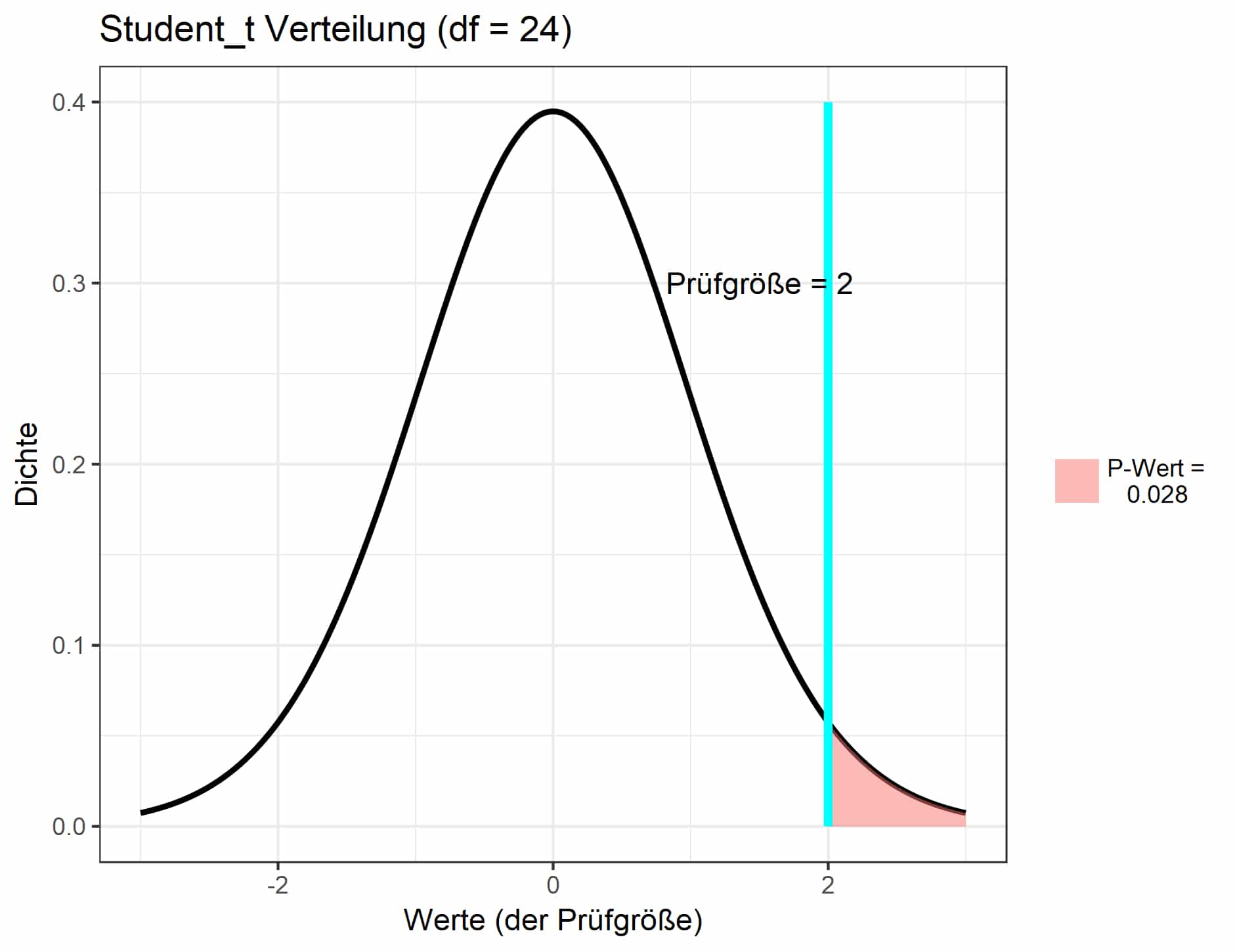
Beispiel 2:
Abb. 6: P-Wert im zweiten Beispiel (rot).
Testentscheidung für statistische Tests
Die Testentscheidung für statistische Tests kann nun sowohl über den Ablehnbereich als auch über den P-Wert herbeigeführt werden. Beim Ablehnbereich verwerfen wir die Nullhypothese und nehmen die Alternativhypothese an, wenn die Prüfgröße in den Ablehnbereich fällt. Zum selben Ergebnis kommst du, wenn der P-Wert kleiner als das Signifikanzniveau ist. Beides trifft immer gemeinsam zu, womit ein Weg vollkommen ausreichend ist. Beide Berechnungen können, so wie es bei der SPSS Clusteranalyse der Fall ist, mit der SPSS Software umgesetzt werden. Wichtig: Liegt die Prüfgröße nicht im Ablehnbereich bzw. der P-Wert ist größer als das Signifikanzniveau bedeutet dies NICHT, dass die Nullhypothese angenommen wird! Dies ist eine häufige Fehlinterpretation. Es kann beispielsweise sein, dass es einen signifikanten Zusammenhang gibt, dieser aber erst bei einer größeren Stichprobe sichtbar (signifikant) wird.
Beispiel 1:
Prüfgröße nicht im Ablehnbereich und P-Wert > 0.05. Die Nullhypothese kann nicht verworfen werden. Eine signifikante Abhängigkeit von Geschlecht und Beförderung kann nicht nachgewiesen werden.
Beispiel 2:
Prüfgröße liegt im Ablehnbereich bzw. P-Wert < 5%. Die Nullhypothese wird verworfen und die Alternativhypothese zu einem Signifikanzniveau von 5% angenommen. Die Verkäufe sind signifikant angestiegen.
Statistische Tests können in Studium für empirische Arbeiten und im Beruf ein treuer Begleiter sein und geben deinen Argumenten eine überzeugende wissenschaftliche Note. Es gibt viele weitere Tests für andere Fragestellungen. Wenn Du Dich jedoch einmal an statistische Tests und deren Ablauf gewöhnt hast, solltest du auch mit anderen Tests keine Probleme haben. Wie immer gilt: Übung macht den Meister! Trotzdem kannst du dich jederzeit an einen Statistik Service wenden, wenn du Fragen hast.
Literatur
Zucchini, Walter. et al (2009): Statistik für Bachelor- und Masterstudenten. Eine Einführung für Wirtschafts- und Sozialwissenschaftler, Heidelberg.