Statistische Verfahren sind alle Methoden, die Dir helfen, Deine Hypothesen zu untersuchen. Welche dieser Verfahren für Dich sinnvoll sind, hängt auch von Deinen Daten ab. Deshalb solltest Du im ersten Schritt einen genauen Blick darauf werfen. Wir erklären Dir im Folgenden statistische Verfahren, wo man sie findet und wie man sie anwendet.
Was sind statistische Verfahren?
Deskriptive Statistik bedeutet, deinen Datensatz durch verschiedene Methoden zu beschreiben. Dabei kannst Du Kennzahlen wie Lage- und Streuungsparameter oder Graphiken nutzen. Während Deine Fragestellung hier noch keine große Rolle spielt, ist die Struktur Deiner Daten wichtig. Sind sie diskret oder stetig; nominal, ordinal, oder metrisch skaliert? Oft bieten sich hier verschiedene Verfahren an. Wenn du dir im Unklaren bist, kann ein Datenanalyse-Service helfen.
Lageparameter
Lagemaße wie Mittelwert, Median und Modus helfen dir, die zentrale Tendenz deines Datensatzes zu ermitteln. Sehen wir uns das mithilfe von Tabelle 1 an.
Tabelle 1: Alter der Probanden (n=7) Quelle: Eigene Darstellung
Diese beschreibt die Altersverteilung einer kleinen Stichprobe (n=7). Dabei ergibt sich ein Mittelwert von 24,42 und ein Median von 22. Der Modus liegt ebenfalls bei 22. Die Differenz zwischen Median und Mittelwert deutet darauf hin, dass die Verteilung nicht symmetrisch ist. Wenn Du diese Vermutung bestätigen möchtest, kannst Du beispielsweise die Schiefe ermitteln.
Streuungsparameter
Streuungsmaße helfen Dir, die Breite Deiner Verteilung einzuschätzen. Dabei sind Varianz und Standardabweichung wichtige Maßzahlen und voneinander abhängig. Erstere beschreibt die quadratische Abweichung vom Mittelwert, letztere errechnet sich aus der Wurzel dieses Werts. Zum Beispiel ergibt sich für Tabelle 1 eine Varianz von 84,95. Daraus folgt eine Standardabweichung in Höhe von 9,21. Einzeln betrachtet sind beide Kennzahlen schwer zu interpretieren. Sie eigenen sich aber gut, um Verteilungen miteinander zu vergleichen.
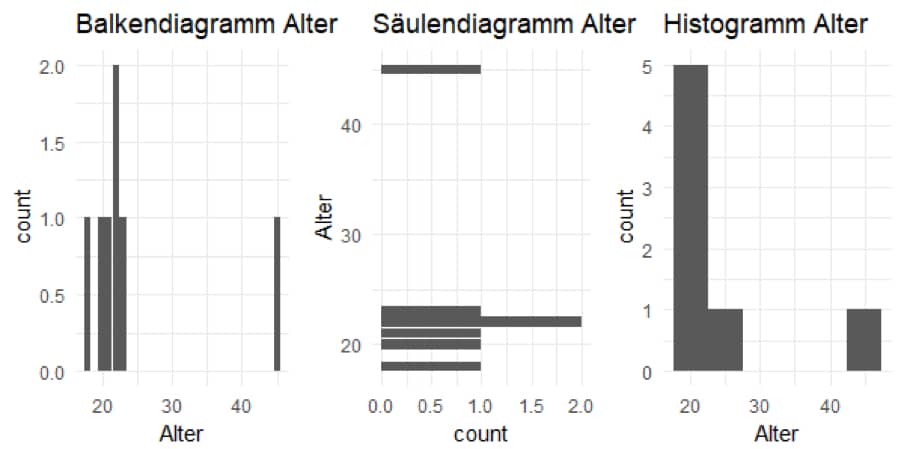
Statistische Verfahren zur grafischen Darstellung deiner Daten
Um Deine statistischen Daten grafisch darzustellen, kannst Du viele statistische Verfahren nutzen. Für unser Beispiel bieten sich Säulen- und Balkendiagramme an. Auch ein Histogramm ist denkbar, wegen der kleinen Stichprobe aber eher ungeeignet.
Abb. 1: Statistische Verfahren: Diagramme für die Variable „Alter“, Quelle: Eigene Darstellung
Möchtest Du mehr als eine Variable betrachten, bietet sich ein Punkteplot an. Dagegen kannst Du Veränderungen über die Zeit durch Liniendiagramme darstellen. Box- und Mosaikplots enthalten hingegen mehr Informationen, sind aber auch schwerer zu interpretieren.
Prüfen von Hypothesen mit Hilfe statistischer Verfahren
Die deskriptive Analyse Deiner Daten ist meistens nur der erste Schritt. In der Regel hast Du bereits konkrete Hypothesen, die Du ablehnen oder untermauern möchtest. Auch dabei kannst Du verschiedene Verfahren nutzen. Nun zählt nicht mehr nur die Struktur Deiner Daten, sondern auch Deine Fragestellung. Interessierst Du Dich für Zusammenhänge oder Unterschiede? Vergleichst Du Varianzen oder Mittelwerte? Sind Deine Zusammenhänge gerichtet oder ungerichtet? Korrelationen in SPSS werden oft für Zusammenhangshypothesen verwendet. Bei Schwierigkeiten kann Dir ein Statistik-Service behilflich sein.
Statistische Verfahren für Unterschiedshypothesen
Betrachten wir erneut das Alter der Probanden aus Tabelle 1.
Jetzt befragen wir eine zweite Gruppe und erhalten Tabelle 2.
Tabelle 2: Alter der Probanden einer zweiten Testgruppe, Quelle: Eigene Darstellung
Angenommen Du interessierst Dich dafür, ob sich das mittlere Alter der beiden Gruppen unterscheidet. Kennst Du die Varianz deiner Grundgesamtheit, bietet sich ein Gaußtest an. Musst Du sie erst schätzen, ist ein t-Test das Richtige. Beide Verfahren setzen metrische, annähernd normalverteilte Variablen voraus. Falls das nicht gegeben ist, solltest Du sogenannte nicht-parametrische Verfahren anwenden. Ein Beispiel dafür ist der Wilcoxon-Mann-Whitney-Test. Für alle diese Verfahren eignet sich übrigens das Statistikprogramm R hervorragend.
Wenn du aus deinem Datensatz Ähnlichkeitsstrukturen herausarbeiten möchtest, dann empfiehlt sich eine Clusteranalyse mit SPSS. Für den Vergleich von mehr als zwei Gruppen, solltest Du die Varianzanalyse nutzen. Deren nicht-parametrische Alternative ist der Kruskal-Wallis-Test. Für nominale Variablen gibt es den Chi-Quadrat-Unabhängigkeitstest, sofern Deine Stichprobe groß genug ist. Andernfalls ist der Exakte Fisher-Test geeignet. Interessierst Du Dich dagegen für Unterschiede in der Varianz, solltest Du dir den F-Test ansehen.
Zusammenhänge mit statistischen Verfahren prüfen
Im vorherigen Abschnitt wurde das Alter mehrerer Gruppen miteinander verglichen. Manchmal möchtest Du dagegen etwas über den Einfluss einer Variablen auf eine andere erfahren, zum Beispiel den Zusammenhang des Alters auf das Gehalt. In diesem Fall musst Du statistische Verfahren zur Analyse von Zusammenhängen nutzen. Beliebt sind hier vor allem Korrelation in SPSS und Statistische Regression.
Korrelation
Korrelationen sind wichtig, wenn Du den Zusammenhang von genau zwei Variablen betrachtest. Dabei ist es egal, welche Variable abhängig und welche unabhängig ist. Sind beide Variablen metrisch skaliert, nutzt Du die Korrelation nach Pearson, die Stärke und Richtung des linearen Zusammenhangs ermittelt. Ist jedoch mindestens eine Variable ordinal, sind Spearman’s rho oder Kendall’s tau gefragt.
Regression
„Regression“ beschreibt eine ganze Reihe von Verfahren. Eine häufige Variante ist die multiple Regression. Hier modellierst Du den linearen Einfluss mehrerer unabhängiger Variablen auf eine abhängige Variable. Dabei können deine UVs metrisch, ordinal, oder sogar nominal sein, deine AV ist metrisch. Es gibt aber auch generalisierte Regressionsmodelle. Diese nimmst Du bei nicht-metrischen AVs, oder wenn Du denkst, Dein Einfluss sei nicht linear. Ein Beispiel dafür ist die logistische Regression. Du nutzt sie bei binären AVs, also Variablen mit nur zwei Ausprägungen.
Zum Prüfen Deiner Hypothesen stehen Dir viele statistische Verfahren zur Verfügung. Im Artikel hast Du einige davon kennengelernt. Es kann aber auch sein, dass Du für Deine Daten und Hypothesen andere Verfahren brauchst, zum Beispiel Methoden zur Analyse von Zeitreihen oder Lebensdaueranalyse, zum Clustering, für die Faktoren- und Hauptkomponentenanalyse. Es gibt auch Methoden, mit denen Du vorab die benötigte Stichprobengröße ermitteln kannst.
Bei der Fülle an Möglichkeiten verliert man schon mal den Überblick. Deshalb bietet die FernUni Schweiz ein Tool an, das dir bei der Auswahl der richtigen Verfahren hilft. Eine Statistik-Beratung kann dir außerdem unter die Arme greifen, wenn du in der Klemme steckst.
