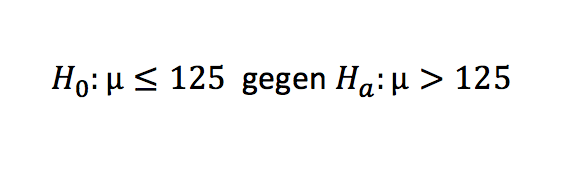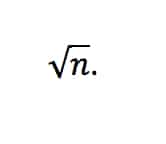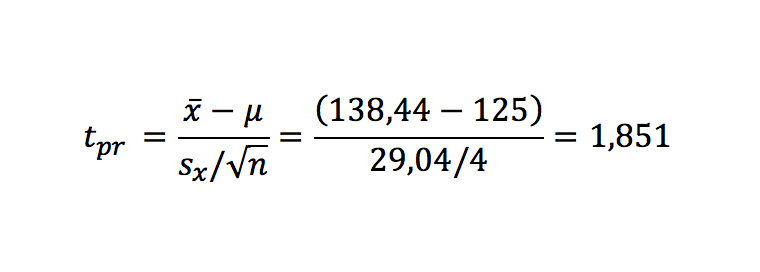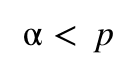Der t-Test prüft ganz allgemein anhand Deiner Stichprobe(n) Hypothesen zu Mittelwertunterschieden in der zugehörigen Grundgesamtheit. Damit Du ihn einsetzen kannst, musst Du für die metrische Zufallsvariable(n) der Grundgesamtheit die Normalverteilung voraussetzen, ohne aber ihre Varianz zu kennen. Bei großen Stichproben, je nach Auslegung ab dreißig oder ab einhundert Beobachtungen, ist diese Bedingung jedoch über den Zentralen Grenzwertsatz automatisch gegeben (siehe auch die Definition bei spektrum.de).
Damit verwendest Du den t-Test im Allgemeinen für solche Situationen, bei denen Du Hypothesen über Mittelwertunterschiede prüfen möchtest, bei denen aber der Gausstest wegen der dann unbekannten Varianz der Grundgesamtheit nicht einsetzbar ist.
Wozu braucht man den t-Test?
Hier soll anhand einer kleinen medizinischen Erhebung kurz und knapp konkretisiert werden, wofür und wie Du den t-Test einsetzen kannst:
Ein Arzt stellt letzthin bei einer Reihe von Patienten, 9 Frauen und 7 Männern, einen erhöhten Laborwert Triglycerid (Tg) fest, von dem er bereits weiß, dass er in der Grundgesamtheit normalverteilt ist. Er vermutet, dass dieser Wert beispielsweise durch Gewichtsabnahme verringert werden kann. Es gelingt ihm, alle 16 Patienten zu einer Diät zu bewegen und er notiert die Tg-Werte aller Personen vor und nach der Abnahme. Er gibt seinen Datensatz schließlich direkt in die SPSS Software ein; dessen Beginn lautet:
| Lfd. Nummer | Geschlecht | Tg-Wert vor Diät | Tg-Wert nach Diät | Abnahme |
| 1 | männlich | 180 | 100 | 6 |
| 2 | weiblich | 142 | 92 | 7 |
| 3 | männlich | 156 | 97 | 5 |
| 4 | ... | ... | ... | ... |
Du sollst jetzt prüfen,
- ob erstens die anfänglichen Tg-Werte signifikant höher als der Normwert 125 sind (Einstichprobenfall)
- inwieweit sich zweitens die anfänglichen Tg-Werte von Männern und Frauen in der Tat signifikant unterscheiden (zwei unabhängige Stichproben) und
- ob drittens in der gesamten Erhebung eine signifikante Reduzierung der Tg-Werte durch die Diät erfolgte (zwei abhängige Stichproben).
Der t-Test als Einstichprobentest
Zunächst prüfst Du, ob die Annahme eines gegenüber dem Normwert von 125 im Mittel erhöhten Triglycerin-Wertes in der Stichprobe vor Durchführung der Diät tatsächlich gerechtfertigt ist.
Du wählst dazu entsprechend im SPSS-Menü den passenden Menüpunkt: Analysieren/Mittelwerte vergleichen/t-Test bei einer Stichprobe:
Abb. 1: Menüwahl für den t-Test bei einer Stichprobe
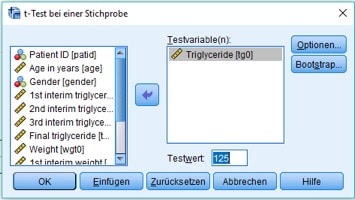
Anschließend gibst Du im sich öffnenden Fenster dann die Testvariable tg0 und den Dich aktuell interessierenden Grenzwert von 125 ein:
Abb. 2: Dialogbox für den t-Test bei einer Stichprobe
Nun klickst Du nur noch auf OK. Blitzschnell erhältst Du dann Dein Testergebnis (siehe hierzu auch die Hinweise der Kent State University).
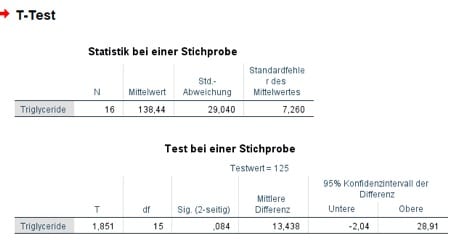
Abb. 3: SPSS-Testergebnis für den t-Test mit einer Stichprobe
Interpretation der Ergebnisse
Um dieses nun interpretieren zu können, musst Du ein wenig in die statische Theorie einsteigen (vgl. Janssen/Laatz 2017).
Laut unserer obigen Annahme ist der Triglycerin-Wert von Patienten in der Grundgesamtheit ja normalverteilt, sowohl mit unbekanntem Mittelwert als auch mit unbekannter Varianz. Im oberen Teil der Testausgabe siehst Du für beide Parameter direkt die Schätzwerte aus Deiner Stichprobe vom Umfang
n=16 als Mittelwert
x = 138,44
und Standardabweichung sx = 29,04.
Du möchtest nun daran Deine Vermutung prüfen, ob der Tg-Wert der Grundgesamtheit in der Tat höher als 125 liegt. Beim Testen von einseitigen Hypothesen formulierst Du dazu Deine Nullhypothese immer umgekehrt zu Deiner Vermutung.
Damit begrenzt Du die Wahrscheinlichkeit, den eigentlich interessierenden Laborwert irrtümlich für erhöht zu halten, auf die im Vorfeld gewählte Fehlerwahrscheinlichkeit 1. Art. (vgl. dazu Martens 2014). Bei Unklarheiten ist die Statistik Nachhilfe ratsam.
Zunächst gehst Du hierzu von einem theoretischen Mittelwert von 125 aus, den Du dann von Deinem Stichprobenmittelwert subtrahierst. Diese Differenz teilst Du danach durch den Schätzwert der Stichprobenvarianz, dividiert durch
Prüfwert ist t-verteilt?
Der dadurch erhaltene Prüfwert ist t-verteilt, mit
(n-1) =15
Freiheitsgraden. Das heißt, wenn der wahre Mittelwert der Grundgesamtheit tatsächlich bei 125 liegt, dann besitzt eine Prüfgröße von Null auch die höchste Wahrscheinlichkeitsdichte, in einer Stichprobe realisiert zu werden. Für Prüfwerte größer oder kleiner als Null nimmt die Wahrscheinlichkeitsdichte entsprechend nach beiden Seiten hin glockenförmig ab.
Für statistische Tests benötigst Du nun die (theoretische) Signifikanz p, bei der der obige Prüfwert gerade eben zum Verwerfen Deiner Hypothese führen würde. Du triffst dann Deine Entscheidung, die Nullhypothese zu verwerfen, wenn
Die SPSS Syntax gibt unter der Beschriftung „Sig. (2-seitig)“ weiterhin den p-Wert für einen zweiseitigen Test, hier mit 0,084 aus; für einen einseitigen Test dagegen wie in Deinem aktuellen Beispiel halbierst Du diesen Wert zu
p=0,084/2=0,042.
Hier wird folglich die Nullhypothese verworfen, denn der p-Wert ist mit 0,042 kleiner als die vorher dazu gewählte Irrtumswahrscheinlichkeit 0,05.
Du kannst dem Arzt also abschließend mitteilen, seine Stichprobe lasse indessen wie erwartet einen erhöhten Triglycerin-Wert vermuten.
t-Test als Zweistichprobentest für unverbundene Stichproben
Im zweiten Fall möchtest Du jetzt durch statistische Verfahren prüfen, ob sich die anfänglichen Triglycerin-Werte von Männern und Frauen signifikant unterscheiden. Da die Werte der beiden Stichproben ja an unterschiedlichen Personen erhoben werden, verwendest Du hier den t-Test für zwei unabhängige Stichproben.
Deine Nullhypothese, die Du wieder mit einer Irrtumswahrscheinlichkeit
α=0,05
testen möchtest, lautet jetzt:
H0: der mittleren Laborwert von Männern und Frauen ist gleich.
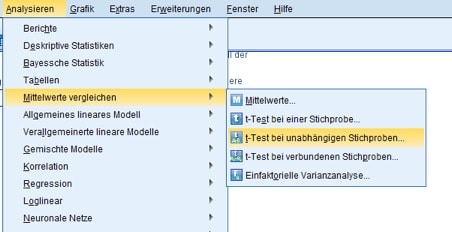
Für die SPSS-Analyse wählst Du dieses Mal im Menü dazu Analysieren/Mittelwerte vergleichen/t-Test bei unabhängigen Stichproben.
Abb. 4: Menüwahl für den t-Test bei unabhängigen Stichproben
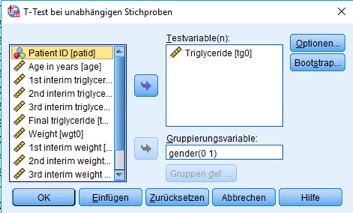
In dem sich in der Folge öffnenden Fenster gibst Du die Testvariable wie bisher als tg0 an, darüber hinaus dient jetzt als Gruppierungsvariable in die beiden Stichproben das Geschlecht (gender).
Abb. 5: Dialogbox beim t-Test bei unabhängigen Stichproben
Du erhältst daraus Deine Testergebnisse:
Abb. 6: Testergebnis beim t-Test mit unabhängigen Stichproben
Im oberen Teil sind wieder wie bei der ersten Analyse Mittelwerte und Standardabweichungen beider Teilstichproben berechnet.
Der t-Test bei unabhängigen Stichproben ist indessen nur dann anwendbar, wenn die Varianzen der Stichproben auch als gleich angenommen werden können. Dies testet der Levene-Test dann auf Varianzgleichheit automatisch im vorderen Bereich der Testergebnisse:
Mit einer Signifikanz von
p=0,440,
die hier schließlich deutlich höher als die übliche Irrtumswahrscheinlichkeit von 0,05 ist, sprechen Deine Stichproben in der Tat nicht gegen die Annahme gleicher Varianzen.
Damit kannst Du anschließend den t-Wert aus der oberen Zeile mit
tpr=1,439
entnehmen und folglich die zugehörige Signifikanz von
p=0,172.
Du verwirfst dieses Mal die Nullhypothese nicht, denn Deine Irrtumswahrscheinlichkeit
α=0,05
ist kleiner als der berechnete p-Wert. Da Du hier einen zweiseitigen Test durchführst, musst Du den p-Wert ja nicht halbieren.
Triglycerin-Werte von Männern und Frauen weisen zumindest nach der erhobenen Stichprobe dementsprechend keine signifikanten Unterschiede auf.
t-Test als Zweistichprobentest für verbundene Stichproben
Werden dagegen Paare von Beobachtungen an jeweils einer Person erhoben, so liegen dann verbundene Stichproben vor. Hier werden die individuellen Triglycerin-Werte zuerst vor und dann nach der Diät an allen Patienten erhoben und es soll daran untersucht werden, ob der Laborwert im Mittel tatsächlich gesunken ist. Der Statistik-Service greift Dir hier unterstützend unter die Arme und beseitigt etwaige Zweifel.
Deine Nullhypothese formulierst Du dann wie immer umgekehrt zu Deiner Vermutung als
H0: Die Laborwerte sind im Durchschnitt gestiegen.
Dazu wählst Du die Irrtumswahrscheinlichkeit
α=0,05,
die Du später wegen des einseitigen Tests mit dem halbierten von SPSS berechneten Signifikanzniveau vergleichst.
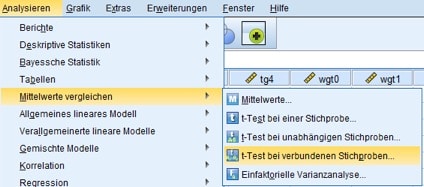
Für Deine SPSS-Analyse wählst Du in diesem Fall den Menübefehl: Menü Analysieren/Mittelwerte vergleichen/t-Test bei verbundenen Stichproben.
Abb. 7: Menüwahl für den t-Test bei verbundenen Stichproben
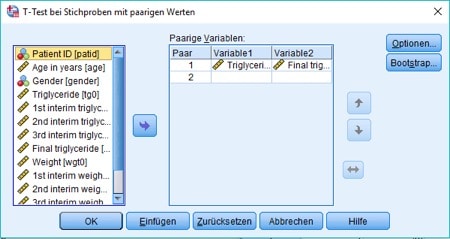
Im nächsten Fenster gibst Du dann die beiden jetzt zu berücksichtigen Variablen an, also den Laborwert vor und nach der Diät.
Abb. 8: Dialogbox für den t-Test bei verbundenen Stichproben
Daraus erhältst Du dementsprechend nachfolgend Deine Analyse:
IMG
Abb. 9: Testergebnis für den t-Test bei verbundenen Stichproben
Das Testergebnis
Im oberen Bereich Deiner jetzigen SPSS-Analyse sind also wieder Mittelwert und Standardabweichung der Werte vor und nach der Diät berechnet. Im mittleren Bereich findest Du dann zusätzlich Angaben zur Korrelation, die mit
0,283 > 0,05
tatsächlich signifikant von Null verschieden ist. Im unteren Bereich schließlich steht der eigentliche Test: SPSS ermittelt das mittlere Absinken des Tg-Wertes und dessen Standardabweichung, sowie Deine daraus folgende Prüfgröße t und die zugehörige Signifikanz.
Da Du hier wieder einseitig testest, musst Du für den relevanten p-Wert die berechnete Signifikanz halbieren: Mit
α=0,05 < 0,124 = p
verwirfst Du die Nullhypothese und schließt folglich auf einen reduzierten Laborwert.
Die Ergebnisse der Stichprobe sprechen demnach also für die anfangs aufgestellte Vermutung des Arztes, dass Gewichtsverminderung in der Tat zu einer Reduzierung des Triglycerinwertes führt.
Egal also, welche der drei Varianten des t-Tests für Deine jeweilige Anwendung die hierfür geeignete SPSS-Analyse darstellt: Berechnung und Interpretation lassen sich in jedem Fall mit der Software durchführen. Alternativ bietet sich natürlich auch der Datenanalyse Service an.
Literatur
Janssen, Jürgen, Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage Berlin.
Martens, Jul (2014): Statistische Datenanalyse mit SPSS für Windows, 2. Auflage Berlin.