Signifikanz – was bedeutet das eigentlich? „Die Ergebnisse sind signifikant“ ist schließlich ein häufig gelesener Satz in wissenschaftlichen Veröffentlichungen. Die kurze Antwort lautet: Die Ersteller der Studie halten (vorerst) an ihrer Forschungshypothese fest. Die etwas längere Antwort: Ihre Ergebnisse sind mit einer gewissen Irrtumswahrscheinlichkeit nicht zufällig. Die ausführliche Antwort erfährst Du in den folgenden Abschnitten.
Wofür brauche ich statistische Signifikanz?
Angenommen, für eine Deiner Vorlesungen werden zwei Übungsgruppen angeboten, die von verschiedenen Dozenten geleitet werden. Natürlich möchtest Du in die Gruppe mit den besten Ergebnissen. Also erhebst Du Daten von ehemaligen Studierenden und erhältst am Ende Tabelle 1.
Tabelle 1: Klausurnoten und Gruppenzugehörigkeit
Berechnest Du nun den jeweiligen Mittelwert der Gruppen, so ergibt sich für die Studierenden von Gruppe A ein Notenschnitt von 2,53 und für die von Gruppe B ein Schnitt von 3,23. Das spricht zunächst für Gruppe A. Allerdings hast Du nur eine (sehr kleine) Stichprobe gezogen. Vielleicht sind dabei in Gruppe A gute, in Gruppe B schlechte Studierende gelandet. Kurzum: Woher willst Du wissen, dass der Notenunterschied nicht zufällig ist?
Was ist statistische Signifikanz?
Theoretisch soll Dir Signifikanz helfen zu entscheiden, ob eine Hypothese plausibel ist. In der Praxis möchte man einen statistischen Kennwert konstruieren, der die Wahrscheinlichkeit angibt, dass der von Dir beobachtete Effekt nicht zufällig ist. Das lässt sich allerdings erstaunlich schwer berechnen. Weder kennen wir die Verteilung der Grundgesamtheit, noch deren Parameter. Das Problem: Wie wollen wir eine Aussage über die Zufälligkeit eines Effekts treffen, wenn wir die wahren Werte gar nicht kennen? Die Lösung: Wir drehen die Fragestellung um!
Der Weg zur statistischen Signifikanz
Damit wir das oben beschriebene Problem vermeiden, fragen wir uns nicht länger „Mit welcher Wahrscheinlichkeit stimmt meine Hypothese?“, sondern „Angenommen, meine Hypothese stimmt nicht. Wie wahrscheinlich ist es, dennoch einen Effekt zu beobachten, der für sie spricht?“.
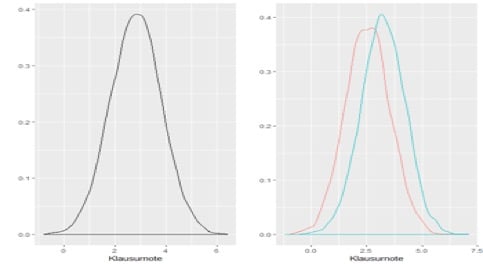
Abbildung 1: Mögliche Verteilung der Klausurnoten
Abbildung 1 zeigt unsere beiden konkurrierenden Hypothesen für die Notenverteilung der Studierenden. Links existiert kein Gruppenunterschied – beide Gruppen haben dieselbe Verteilung. Rechts ist dagegen der Erwartungswert von Gruppe A niedriger. Sie bekommt also bessere Noten. Die Frage lautet nun: „Angenommen, die linke Grafik stimmt. Wie wahrscheinlich ist es, Daten zu erheben, die für die rechte Grafik sprechen?“ Und was muss gegeben sein, damit die statistische Analyse belastbar ist?
Null- und Alternativhypothese
Formaler ausgedrückt arbeiten wir zwar weiterhin mit unserer Forschungshypothese, versuchen aber nicht mehr ihre Wahrscheinlichkeit zu berechnen, sondern konzentrieren uns auf das Gegenteil.
Jetzt wird es etwas kompliziert: Unsere eigentliche Hypothese (die beiden Gruppen sind verschieden) wird zur Alternativhypothese, auch H1 genannt. Ihr Gegenstück, also das, wovon wir eigentlich nicht ausgehen, ist die Nullhypothese H0. In unserem Fall lautet H0: „Die Noten der beiden Übungsgruppen unterscheiden sich nicht“. Daraus ergibt sich für H1: „Die beiden Gruppen unterscheiden sich“. Damit können wir die am Ende des letzten Abschnitts gestellte Frage verallgemeinern: „Angenommen H0 gilt. Wie wahrscheinlich ist es, statistische Daten zu beobachten, die mindestens so stark für H1 sprechen wie unsere?“
Abhängig von dem Ergebnis, behalten wir H0 bei oder lehnen die Hypothese ab. Aber Achtung: Wahrscheinlichkeiten sind keine Beweise! Die Statistik Nachhilfe kann hier für mehr Klarheit sorgen.
Fehler 1. und 2. Art
Da wir mit Zufallsstichproben arbeiten, werden wir nie 100%ige Sicherheit erreichen. Dementsprechend können auch statistische Tests auf Signifikanz falsche Ergebnisse liefern.
Wir sprechen dabei von den Fehlern 1. und 2. Art. Abbildung 2 zeigt Dir, was diese bedeuten.
Abbildung 2: Fehler 1. und 2. Art für statistische Signifikanz
Im Grunde können wir mit unserer Schlussfolgerung also auf zwei Arten falschliegen.
- Wir verwerfen unsere Nullhypothese, obwohl sie richtig gewesen wäre (Fehler 1. Art)
- Wir akzeptieren unsere Nullhypothese, obwohl sie falsch ist (Fehler 2. Art).
Um bei unserem Beispiel zu bleiben, können wir also entweder von einem Gruppenunterschied ausgehen, obwohl dieser gar nicht existiert. Oder wir lehnen H0 ab, in Wahrheit unterschieden sich die beiden Gruppen aber sehr wohl.
Natürlich können wir den Fehler 1. Art vermeiden, indem wir H0 einfach immer annehmen. Dabei begehen wir aber irgendwann zwangsweise den Fehler 2. Art. Die beiden Fehler hängen also zusammen. Da wir in irgendeinen sauren Apfel beißen müssen, entscheiden wir uns für den, dessen Wahrscheinlichkeit wir aktiv beeinflussen können. Den Fehler 1. Art.
Wie bestimme ich statistische Signifikanz?
In den letzten Abschnitten haben wir viel darüber erfahren, was Signifikanz eigentlich ist. Offen ist noch, wie Du diese ermittelst. Eine Pauschallösung gibt es dabei allerdings nicht. Die exakte Bestimmung ist von Deinen Daten, der Fragestellung und weiteren Faktoren abhängig (vgl. Fahrmeier et al., 2012). Alternativ kann dies der Datenanalyse Service entweder mit Dir gemeinsam oder für Dich übernehmen.
Drei Größen werden dabei aber immer eine Rolle spielen: Effektstärke, Streuung und Stichprobengröße. Eine große Notendifferenz zwischen den beiden Gruppen spricht eher für H1. Mit wachsender Effektstärke sinkt also die Wahrscheinlichkeit, dass dennoch H0 gilt. Eine starke Streuung sorgt hingegen für mehr Unsicherheit. Schließlich gibt es noch die Stichprobengröße. Auch hier gilt, dass eine große Stichprobe eher signifikante Ergebnisse liefert als eine kleine Stichprobe. Allerdings haben Wood et al. gezeigt, dass mit einer reinen Erhöhung der Stichprobengröße ein zuvor insignifikantes Ergebnis nicht zwingend signifikant wird (vgl. Wood et al, 2014).
Alle drei Größen kannst Du anhand Deiner erhobenen Daten im Zuge einer Datenanalyse ermitteln. Im zweiten Schritt berechnest Du die Wahrscheinlichkeit, die von Dir beobachtete Effektstärke (oder eine, die noch stärker zur Alternativhypothese tendiert) zu erhalten, obwohl H0 gilt. Diese Wahrscheinlichkeit vergleichst Du schließlich mit dem zuvor von Dir festgelegten Signifikanzniveau. Dieses entspricht Deinem Risiko, die Nullhypothese abzulehnen, obwohl sie stimmt (Fehler 1. Art). Angenommen, in unserem Beispiel läge die Wahrscheinlichkeit, eine Differenz von 0,7 Notenpunkten zu beobachten, wenn eigentlich kein Unterschied existiert, bei 17%. Wie würdest Du dich entscheiden?
Tücken der statistischen Signifikanz
In Studien wird meist bei einer Irrtumswahrscheinlichkeit von unter 5% von einem signifikanten Ergebnis gesprochen. Gelegentlich machen Autoren oder Leser den Fehler, die Alternativhypothese damit als bewiesen anzusehen. Dass das so nicht richtig ist, haben wir gerade gelernt.
Ein Signifikanzniveau von 5% bedeutet lediglich, 5% Irrtumswahrscheinlichkeit als akzeptabel zu betrachten. Das ist auch durchaus in Ordnung, solange wir nur einen einzigen Test durchführen. Stell Dir aber vor, wir testen Gruppenunterschiede für 20 Vorlesungen. Was denkst Du, wie hoch die Wahrscheinlichkeit ist, bei einem Signifikanzniveau von 5% H0 mindestens einmal fälschlich abzulehnen? Es sind ganze 64%.
Statistische Signifikanz wird sogar so häufig falsch interpretiert, dass die American Statistical Association 2016 ein Statement dazu veröffentlicht hat. Zum Glück weißt Du es jetzt besser.
Statistische Signifikanz hilft Dir, Dich für oder gegen Deine Forschungshypothese zu entscheiden. Ihre konkrete Berechnung ist abhängig von Deiner Hypothese und den vorliegenden Daten, folgt jedoch immer demselben Prinzip. Allerdings musst Du im Anschluss an Deine Auswertung darauf achten, wie Du Deine Ergebnisse interpretierst. Bei Unsicherheiten ist der Statistik-Service ratsam.
Literatur
Fahrmeir, Ludwig/Heumann, Christian/Künstler, Rita/Pigeot, Iris/Tutz, Gerhard (2012): Statistik: Der Weg zur Datenanalyse, 7. Auflage Berlin.
Wood, John/Freemantle, Nick/King, Michael/Nazareth, Irwin (2014): Trap of trends to statistical significance. Likelihood of near significant P value becoming more significant with extra data, in: BMJ (Clinical research ed.) 348, g2215.