Die Varianzanalyse hilft Dir zu untersuchen, ob die Verteilung eines metrischen Merkmals von einem nominalskalierten Merkmal mit mehr als zwei Ausprägungen bestimmt wird – in Anlehnung an die Datenverteilung in SPSS. Du prüfst etwa, ob signifikante Einkommensunterschiede zwischen verschiedenen Branchen bestehen, ob sich die Anzahl der Sonnenstunden in verschiedenen Städten signifikant unterscheidet, usw.
Du wendest sie, anders ausgedrückt, immer dann an, wenn Du mehr als zwei Gruppen auf Unterschiede im Mittelwert testen möchtest, so dass der Gauss-Test oder t-Test nicht angewendet werden kann. Inhaltlich kannst Du sie daher als Verallgemeinerung dieser Verfahren sehen.
Die Durchführung mit der SPSS Software ist ganz einfach.
Idee der Varianzanalyse in SPSS und Vorstellung des Datensatzes
Stell Dir vor, Du hast über deinen Zeitraum von 15 Wochen die Anzahl der Vertragsabschlüsse dreier Vertreter notiert. Du möchtest jetzt prüfen, ob sich der Erfolg der drei Mitarbeiter signifikant unterscheidet.
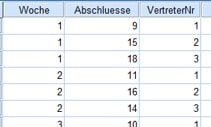
Dein Datensatz sieht dazu wie folgt aus:
Abb. 1: Datensatz mit der Anzahl der Vertragsabschlüsse dreier Vertreter in jeder Woche
Aus diesen Daten berechnest Du Schätzwerte für Erwartungswert und Varianz in der Grundgesamtheit für verschiedene Gruppierungen. Anschließend ermittelst Du daraus für das statistische Verfahren der Varianzanalyse folgende Terme:
- SQT: Summe der quadratischen Abweichungen aller Beobachtungswerte vom Gesamtmittelwert
- SQI: Summe der quadratischen Abweichungen aller Beobachtungswerte von ihrem Gruppenmittelwerte
- SQZ: Summe der quadratischen Abweichungen der Gruppenmittelwerte vom Gesamtmittel, multipliziert mit der Gruppengröße.
In jedem Fall gilt:
SQT = SQI + SQZ
Die totale Summe (SQT) der quadratischen Abweichungen lässt sich also in zwei Summanden aufteilen: Sie ist die Summe aus den quadratischen Abweichungen innerhalb (SQI) und den quadratischen Abweichungen (SQZ) zwischen den Gruppen.
Deine Nullhypothese bei der Varianzanalyse lautet: „Es gibt keine Mittelwertunterschiede zwischen den betrachteten Gruppen, alle Mittelwerte sind in der Grundgesamtheit gleich“. Du testest sie dann gegen die Alternative: „Mindestens ein Mittelwert unterscheidet sich signifikant“.
Nun dividierst Du zuerst die Summanden der Zerlegung durch ihre zugehörigen Freiheitsgrade υ1 und υ2. Deren Quotient ergibt dann Deine Prüfgröße:
Falls die Nullhypothese gilt und Mittelwertunterschiede im Datensatz zufällig bedingt sind, sollte SQZ klein und SQI im Verhältnis dazu groß ausfallen. Daher verwirfst Du die Nullhypothese, falls dein Prüfwert größer als der kritische Wert zur gewählten Irrtumswahrscheinlichkeit α ist. Oder Du vergleichst die von SPSS berechnete Signifikanz p mit α. Die Nullhypothese wird verworfen, falls p kleiner als α ist. Fall sich hierbei Schwierigkeiten für dich ergeben sollten, bietet sich dir die Statistik Nachhilfe.
Eine ausführlichere Darstellung findest Du etwa bei den Ausführungen des Lehrstuhls für Mathematik der Universität Würzburg.
Praktische Durchführung der Varianzanalyse in SPSS
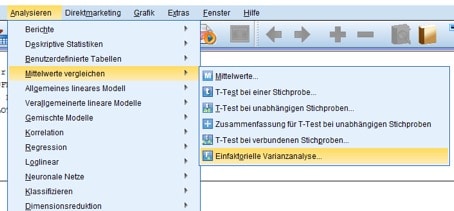
In diesem Beispiel handelt es sich um eine einfaktorielle Varianzanalyse. Es wird also untersucht, ob die mittlere Anzahl (und bei einer Normalverteilungsannahme somit die komplette Verteilung) der Vertragsabschlüsse zwischen den Vertretern variiert. Nach dem SPSS Daten Importieren startest Du die einfaktorielle Varianzanalyse Du über die Menüfolge Analysieren/Mittelwerte vergleichen/Einfaktorielle Varianzanalyse.
Abb. 2: SPSS-Menüfolge für die einfaktorielle Varianzanalyse
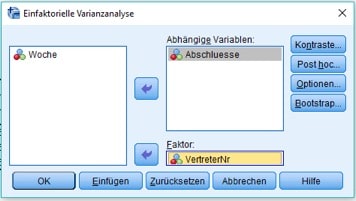
Es öffnet sich eine Dialogbox, in die Du Abschlüsse als abhängige Variable und VertreterNr als Faktor auswählst.
Abb. 3. Dialogbox der einfaktoriellen Varianzanalyse
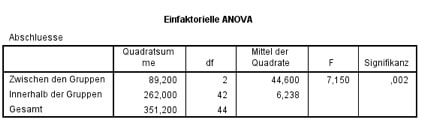
Klicken auf OK ergibt als Output:
Abb. 4: SPSS-Output für die einfaktorielle Varianzanalyse
Wie oben angegeben, triffst Du Deine Testentscheidung, indem Du die berechnete Signifikanz mit der gewählten Irrtumswahrscheinlichkeit α vergleichst: Mit 0,002 kleiner als α=0,05 verwirfst Du die Nullhypothese, es gebe keine Mittelwertunterschiede zwischen den Gruppen. Du schließt also, dass mindestens ein Vertreter signifikant unterschiedlich viele Vertragsabschlüsse als die anderen vorweisen kann. Bei Unsicherheiten empfiehlt sich der Statistik-Service.
Voraussetzungen und Erweiterungen der Varianzanalyse in SPSS
Voraussetzung für die Durchführung einer Varianzanalyse ist zum einen, dass die Beobachtungswerte Deiner abhängigen metrischen Variablen einer Normalverteilung in SPSS unterliegt. Ein üblicher Test hierfür ist der Shapiro-Wilk-Test auf Normalverteilung, den Du in SPSS über die Menüfolge Analysieren/Deskriptive Statistiken/Explorative Datenanalyse findest.
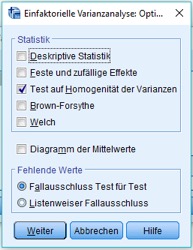
Zum anderen müssen die Varianzen in den Gruppen homogen sein, das heißt, sie müssen die Annahme erlauben, dass eine einheitliche Varianz vorliegt. Statistische Tests wie beispielsweise der Levene-Test eignen sich hierfür, denn Du kannst ihn als ergänzenden Output in der Abb. 3 anfordern. Klicke dafür in der Abb. 3 auf Optionen und Du kannst in der folgenden Dialogbox den Test auf Homogenität der Varianzen anhaken (Vgl. dazu auch Janssen/Laatz, 2017).
Abb. 5: Test auf Homogenität der Varianzen auswählen.
Die SPSS Syntax ist so konzipiert, dass sie Dir dann zusätzlich zu dem oben angegebenen Output die folgenden Angaben liefert:
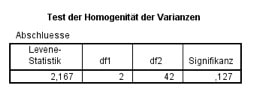
Abb. 6. SPSS-Output für den Levene-Test auf Homogenität der Varianzen
Vergleichst Du im Rahmen der Datenanalyse in SPSS die berechnete Signifikanz mit Deiner Irrtumswahrscheinlichkeit von α=0,05, so kann die Nullhypothese, die Varianzen seien gleich, nicht verworfen werden. Dein Testergebnis spricht damit also nicht gegen die Voraussetzung der Varianzhomogenität.
Möchtest Du den Einfluss von mehr als einer unabhängigen nominalskalierten Variablen auf die abhängige metrische Variable prüfen, so handelt es sich um eine mehrfaktorielle Varianzanalyse. Sie startest Du über die Menüfolge Analysieren/Allgemeines lineares Modell/Univariat. Falls Du den Einfluss auf mehrere abhängige Variablen prüfen möchtest, wählst Du die Menüfolge Analysieren/Allgemeines lineares Modell/Multivariat (Vgl. dazu auch Martens, 2017). Alternativ bietet sich natürlich der Datenanalyse Service an.
Die Varianzanalyse gibt Dir damit also eine Sammlung von Methoden, mit denen Du den Einfluss oder die Abhängigkeit metrisch-skalierter Variablen von nominalskalierten Faktoren prüfen kannst. Sie wird oft eingesetzt, um zu testen, ob sich die Zugehörigkeit zu bestimmten Kategorien oder Gruppen auf messbare Variablen auswirkt.
Literatur
Janssen, Jürgen/ Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage Berlin.
Martens, Jul (2014): Statistische Datenanalyse mit SPSS für Windows, 2. Auflage Berlin.