Korrelation in SPSS untersuchen: Korrelieren zwei Variablen miteinander, bedeutet das, dass sie in Zusammenhang zueinanderstehen. Ursprünglich bezog sich der Begriff Korrelation auf metrische, also mindestens intervallskalierte Variablen. Dann beschreibt eine Korrelation einen linearen Zusammenhang. Diesen kannst du zum Beispiel mit SPSS berechnen, aber nicht nur für diesen Standardfall. Es gibt auch für ordinalskaliere, dichotome oder kategoriale Daten Werkzeuge bei SPSS. Wir schauen uns zunächst den metrischen Fall an. Weiter unten gehen wir auf die nicht-parametrischen Maße ein.
Woraus berechnet sich eine Korrelation in SPSS?
Die Korrelation zwischen zwei Variablen sagt etwas über deren gemeinsame Varianz aus. Das bekannteste Maß für die Korrelation ist der Pearson-Korrelationskoeffizient, auch Produkt-Moment-Korrelation genannt. Dieser Koeffizient gibt an, wie stark der lineare Zusammenhang zwischen beiden Variablen ist. Er berechnet sich aus der Kovarianz, was – genau, Du denkst es Dir schon – die gemeinsame Varianz der Variablen ist. Man kann die Varianz einer Variablen also aufteilen in deren geteilte und ungeteilte Varianz.
Für einen Datensatz mit n Beobachtungen berechnet sich die Kovarianz zwischen den beiden Variablen X und Y aus:
Die Korrelation hat gegenüber der Kovarianz den Vorteil, dass sie standardisiert ist. Der Wert bewegt sich zwischen -1 und 1 und ist somit leicht über verschiedene Studien hinweg vergleichbar. Die Größe der Kovarianz hingegen hängt von der Metrik der Variablen ab, und ist daher schwer zu interpretieren. Hilfe dabei bietet etwa ein Datenanalyse-Service.
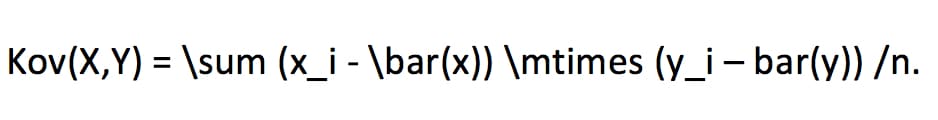
Untersuchung einer Korrelation in SPSS
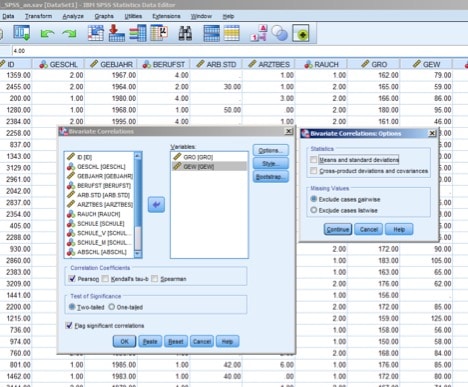
In der SPSS Software findest Du den Befehl für die Pearson-Korrelation im Menü “Analyse” unter „Korrelation“ und dann „Bivariat“. Dann öffnet sich ein Fenster, das so aussieht wie in Abbildung 1.
Abbildung 1: Produkt-Moment-Korrelation in SPSS berechnen
Die Variablen, deren Korrelation Du berechnen möchtest, kannst Du aus der Liste auf der linken Seite auswählen. Auf der rechten Seite sind alle ausgewählten Variablen aufgeführt. SPSS berechnet paarweise die Korrelation zwischen allen ausgewählten Variablen. „Pearson“ ist als Standardkorrelationskoeffizient schon vorausgewählt.
Du kannst also auch mehr als zwei Variablen auswählen. Danach erhältst Du eine Ergebnistabelle mit bivariaten Korrelationskoeffizienten zwischen allen Zweierkombinationen von Variablen. Beachte, dass das etwas anderes ist als eine multiple Korrelation. Das liegt daran, dass SPSS bei der „bivariaten Korrelation“ immer genau zwei Variablen in die Rechnung aufnimmt.
Auf das Skalenniveau achten
Du musst selbst berücksichtigen, dass Deine Daten ein geeignetes Skalenniveau für die Analyse haben. Du kannst nämlich jede numerische Variable auswählen, ohne dass SPSS eine Fehlermeldung ausgibt. Zum Beispiel könntest Du die Variable „RAUCH“ aufnehmen, die mit 1 (= Ja) oder 2 (= Nein) kodiert, ob eine Person raucht oder nicht. SPSS würde wie gefordert die Produkt-Moment-Korrelation ausrechnen. Allerdings ist das Ergebnis mathematisch nicht sinnvoll, da das Intervallskalenniveau ja eine Voraussetzung für die Berechnung ist.
Unter „Optionen“ kannst Du zudem auswählen, ob Du auch die Kovarianzen und deskriptiven Statistiken angezeigt bekommen möchtest. Bootstrap ist eine Möglichkeit, um Konfidenzintervalle für die Korrelationskoeffizienten zu bestimmen. Diese Option bietet SPSS bei fast jeder statistischen Analyse. Im Übrigen bietet diese Software auch die Möglichkeit einer Clusteranalyse mit SPSS.
Wenn Du lieber mit der SPSS Syntax arbeitest, lautet der Befehl für Korrelationen „Correlations“. Dem Befehl musst Du die Variablen übergeben, die Du analysieren möchtest. Für unser Beispiel sieht das so aus:
Korrelation in SPSS darstellen
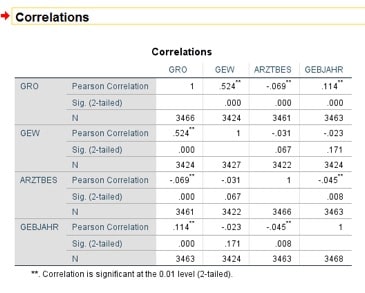
In Abbildung 2 siehst du eine typische Ergebnistabelle für bivariate Korrelationen.
Abbildung 2: Bivariate Korrelationen zwischen Größe, Gewicht, Anzahl der Arztbesuche und Geburtsjahr
Neben dem Korrelationskoeffizienten findest Du auch den p-Wert für den Signifikanztest. Weiterhin erhältst Du N, also die Anzahl der Fälle, die in die Rechnung mit eingegangen sind. N liefert einen ganz guten Überblick darüber, wie viele fehlende Werte in Deinem Datensatz vorliegen. Mithilfe der Sternchen kannst Du alle signifikanten Zusammenhänge schnell erkennen. Nutze einfach unsere Statistik Beratung, falls Du mit Deinen Korrelationsuntersuchungen nicht weiterkommen solltest.
Korrelation für ordinalskalierte Daten
Daten, deren Struktur eine Ordnung hat, bei denen die Abstände zwischen den Klassen aber nicht definiert sind, heißen Rangreihen. Für Rangreihen oder auch ordinalskalierte Daten gibt es zwei häufig verwendete Korrelationsmaße: Spearman’s Rho und Kendall’s Tau. Genauso wie der Pearson-Korrelationskoeffizient beziffern sie die Stärke des Zusammenhangs zwischen -1 und +1.
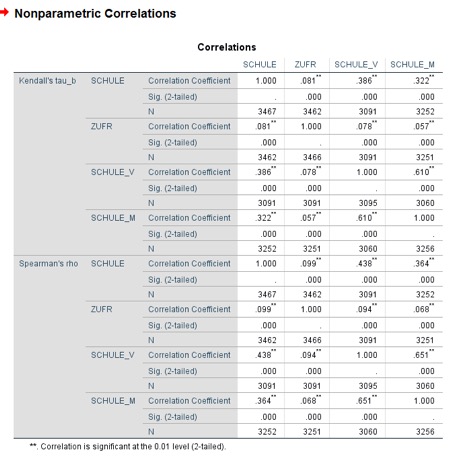
Abbildung 3: Ergebnisbericht in SPSS für Korrelationen zwischen Rangreihen
Die Ergebnistabelle hat die uns schon bekannte Form. Und zwar sind hier zum Vergleich der beiden Maße sowohl die Korrelationen nach Kendall als auch nach Spearman aufgeführt. Du erkennst, dass die Werte für Kendall’s Tau etwas niedriger sind, was typisch ist.
Debatte zu den Methoden
Beide Maße sind anerkannte Methoden, um Rangkorrelationen zu berechnen, dennoch gibt es in der Wissenschaftsgemeinschaft eine Debatte, wann welches geeigneter ist. Kendall’s Tau unterteilt die Wertepaare in konkordante und diskordante Paare ein. Es zählt also wie häufig sich die Rangfolgen zwischen den Variablen widersprechen. Spearman’s Rho berücksichtigt die exakte Rangposition und betrachtet die absoluten Abweichungen der beiden Rangpositionen (Capéraà/Genest, 1993).
Wenn Deine Daten einen Spezialfall darstellen, und nur eines der beiden Maße Signifikanz erreicht, kannst Du Dich genauer informieren, welches die bessere Wahl ist. Meist sollte es kaum Diskrepanzen zwischen Spearman’s Rho und Kendall’s Tau geben. Dann ist die Wahl eine Frage der Vorliebe oder der Gewohnheit.
Du kannst außerdem nicht nur die Korrelation zwischen zwei ordinalskalierten Variablen berechnen, sondern auch zwischen einer ordinalskalierten und einer intervallskalierten Variablen. Kendall’s Tau wird auch gerne bei metrischen Variablen eingesetzt, wenn die Voraussetzungen für die Produkt-Moment-Korrelation nicht erfüllt sind.
Partialkorrelation
Manchmal möchte man den Zusammenhang zwischen zwei Variablen um den Einfluss bestimmter Drittvariablen kontrollieren. Es kann sein, dass sich ein Zusammenhang zwischen zwei Variablen als Scheinzusammenhang entpuppt, der durch eine dritte Größe zustande kommt. Wenn Du so eine Situation vermutest, ist die Partialkorrelation ein nützliches Werkzeug. Mit ihr kannst Du den Einfluss weiterer Variablen herauspartialisieren. Ein Beispiel dazu findest Du übrigens bei der Universität Oldenburg.
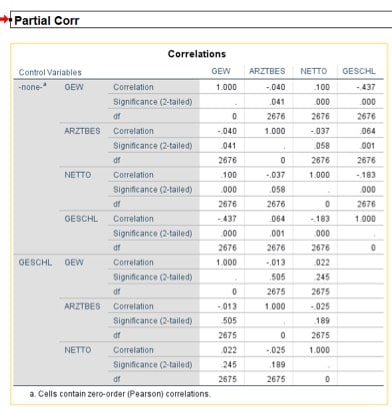
Angenommen, du hast einen signifikanten Zusammenhang zwischen Gewicht und der Anzahl der Arztbesuche gefunden. Auch scheint das Gewicht positiv mit dem Nettoeinkommen zu korrelieren? Kann es sein, dass schwerere Leute seltener zum Arzt gehen und mehr verdienen? Wenn Du das Geschlecht als Kontrollvariable aufnimmst, siehst Du, dass beide Zusammenhänge nicht mehr signifikant sind.
Abbildung 4: Ausgabefenster in SPSS für die Korrelation zwischen Gewicht, Anzahl der Arztbesuche und dem Nettoeinkommen. In der oberen Hälfte sind die reinen Korrelationen, in der unteren sind sie bereinigt um den Einfluss von Gewicht.
Wichtige Warnung
An dieser Stelle erinnern wir an eine wichtige Warnung. Selbst wenn Du Partialkorrelationen berechnest, kannst Du keine Aussage über Kausalität treffen. Aussagekraft zu Kausalität ist eine Eigenschaft des Versuchsdesigns und kann nicht mithilfe von statistischen Methoden hergestellt werden – egal wie ausgefeilt diese sind.
In diesem Artikel haben wir die wichtigsten Zusammenhangsmaße besprochen und wie sie sich bei SPSS berechnen lassen. Natürlich sind eine ganze Reihe anderer Datensituationen denkbar, in denen Du Zusammenhänge analysieren möchtest. Beispiele dafür sind der Zusammenhang zwischen einer dichotomen und einer intervallskalierten Variablen oder zwischen verschiedenen kategorialen Variablen. Für viele dieser Situationen bietet SPSS geeignete Korrelationsanalysen an. Die Homepage der Fernuni Hagen bietet Lernmodule zu kategorialen Maßen.
Literatur
Capéraà, Philippe/Genest, Christian (1993): Spearman’s ρ is larger than kendall’s τ for positively dependent random variables, in: Journal of Nonparametric Statistics 2, 2, S. 183-194.
