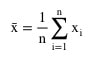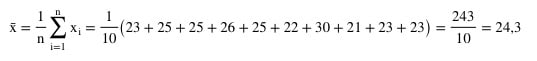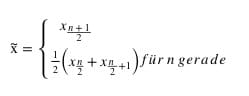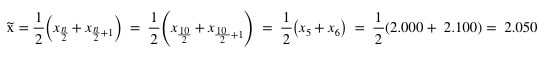Mittelwert bezeichnet das arithmetische Mittel, das eines der wichtigsten Lagemaße in der Statistik ist. Oft musst Du es ganz direkt angeben: Wie hoch ist das mittlere Einkommen in deiner Stichprobe? Wie alt sind die Befragten im Schnitt? Gelegentlich versteckt es sich auch im Hintergrund einer anderen Methode. Hier erfährst Du alles Wichtige zum Mittelwert und lernst zwei wertvolle Alternativen kennen.
Wie wird der Mitterwert berechnet?
Die Berechnung des Mittelwerts ist simpel, bestimmt hast auch Du das schon mal gemacht, zum Beispiel, um deinen Notendurchschnitt zu ermitteln. Im Prinzip addierst Du sämtliche relevanten Werte und teilst das Ergebnis durch die Anzahl der Beobachtungen. Formaler lässt sich der Mittelwert durch folgende Formel darstellen:
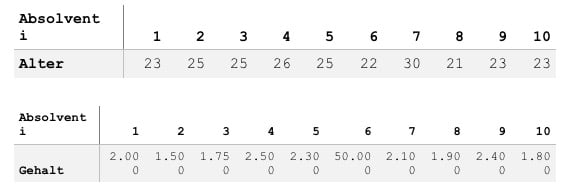
Sehen wir uns das Ganze mit einem Beispiel an. Stelle dir vor, Du interessierst dich für das durchschnittliche Alter von Bachelorabsolventen, also ziehst du eine Zufallsstichprobe mit insgesamt 10 Befragten. Tabelle 1 stellt ihre Antworten dar.
Tabelle 1, Quelle: Eigene Darstellung
Im nächsten Schritt setzen wir diese in die obige Formel ein:
Wir erhalten ein arithmetisches Mittel von 24, 3. Das bedeutet, die Studierenden deiner Stichprobe haben ihren Bachelorabschluss im Schnitt mit 24,3 Jahren erlangt. Wenn du hier Probleme hast, kann dir ein Datenanalyse-Service helfen.
Alternativen zum Mittelwert
So wichtig der Mittelwert in der Statistik ist, er hat seine Tücken. Angenommen, Dich interessiert neben dem Alter auch das mittlere Einstiegsgehalt der Bachelorabsolventen (Tabelle 2). Auf den ersten Blick sieht ein arithmetisches Mittel von 6.825 € ziemlich grandios aus! Bei näherer Betrachtung sticht jedoch Absolvent 6 ins Auge.
Tabelle 2, Quelle: Eigene Darstellung
Was ist passiert? Beim Mittelwert handelt es sich um ein sogenanntes „ausreißerempfindliches Lagemaß“. Das bedeutet, sehr hohe oder sehr niedrige Werte können ihn verzerren, insbesondere dann, wenn Deine Stichprobe eher klein ausfällt. Hier kommt deshalb der Median ins Spiel.
Was ist der Median?
Im Gegensatz zum Mittelwert arbeitet der Median nicht mit den tatsächlichen Werten, sondern mit der Rangfolge dieser Beträge. Deshalb ist es auch egal, ob der Top-Verdiener in deiner Stichprobe 5.000 € oder 50.000 € pro Monat verdient. Er landet so oder so auf dem höchsten Rang. Darauf folgt der zweithöchste Betrag und so weiter, bis die Urliste vom kleinsten zum größten Wert sortiert wurde.
Nun bezeichnet man genau den Wert als Median, der diese Liste in zwei gleichgroße Hälften „teilt“. Das bedeutet, 50% deiner Absolventen verdienen besser oder gleich des Medians und 50% schlechter oder gleich.
Median berechnen
Wie der Mittelwert, lässt sich der Median mit einer Formel darstellen:
Mit ihrer Hilfe können wir für unser Beispiel nun nicht nur ein arithmetisches Mittel für das Einstiegsgehalt bestimmen, sondern auch den Median.
Dafür sortieren wir zunächst die obige Tabelle nach Höhe des Verdienstes (Tabelle 3).
Tabelle 3, Quelle: Eigene Darstellung
Anschließend wenden wir die Formel für den Median an. Da mit zehn Beobachtungen ein gerades n vorliegt, sieht das wie folgt aus:
Nun wird deutlich, dass Mittelwert und Median beim Einkommen weit auseinanderliegen. Da der Median nicht von unserem Ausreißer beeinflusst wird, ist er in diesem Fall ein zuverlässigerer Wert, um abzuschätzen, wie viel Bachelorabsolventen in ihrem ersten Job verdienen.
Der Median kann noch mehr!
Der Median hat noch einen zweiten Vorteil: Er kann auch für ordinalskalierte Variablen verwendet werden. Das sind Variablen, deren Werte sich zwar ordnen lassen, bei denen die Abstände dieser Werte jedoch nicht exakt festgelegt sind. Ein beliebtes Beispiel hierfür sind Schulnoten. Schüler mit Note 2 sind nicht zwingend doppelt so gut wie Schüler mit Note 4. Deshalb ist auch die Berechnung des Mittelwerts nicht sinnvoll, wenn man eine Statistik Beratung fragt. Dass das in der Praxis oft anders gehandhabt wird, hat jeder in der Schule erfahren.
Was ist der Modus?
Apropos Skalenniveau: Hast du schon einmal versucht, den Mittelwert von Studiengängen zu berechnen?
Während der Mittelwert ausschließlich für mindestens intervallskalierte Variablen geeignet ist, kann der Median auch für ordinale Skalen bestimmt werden. Daneben gibt es aber noch die Nominalskala, die keinerlei Aussage über eine Rangfolge zulässt. In diesem Fall helfen uns weder Mittelwert noch Median weiter.
Das führt uns zum letzten Lagemaß der deskriptiven Statistik, das als Alternative für ein arithmetisches Mittel genutzt werden kann: den Modus.
Modus berechnen
Der Modus beschreibt den am häufigsten in unseren Daten vorkommenden Wert und ist so simpel, dass wir dafür nicht einmal eine Formel brauchen.
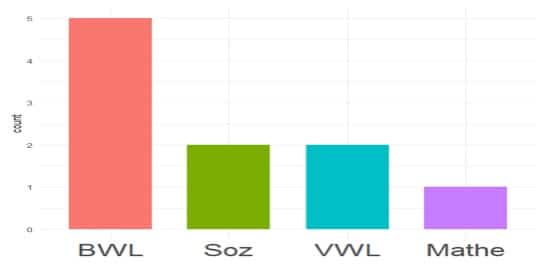
Bleiben wir bei unserem Beispiel und sehen uns die Studiengänge der Bachelorabsolventen näher an.
Tabelle 4, Quelle: Eigene Darstellung
Im Gegensatz zu Mittelwert und Median erkennst Du den Modus hier auf den ersten Blick. BWL wird als einziger Studiengang fünfmal genannt und ist damit der häufigste Wert. Alternativ kannst Du die Häufigkeiten mithilfe einer Kreuztabelle oder eines Balkendiagramms darstellen.
Quelle: Eigene Darstellung
Ein weiterer Vorteil des Modus ist, dass er für jedes Skalenniveau bestimmt werden kann. Du musst Dir also keine Gedanken machen, ob Deine Variablen nominal-, ordinal-, oder intervallskaliert sind. Probleme bekommst Du nur dann, wenn sehr viele verschiedene Merkmalsausprägungen vorliegen.
Der Modus hat auch Nachteile
Betrachten wir nochmal die Tabellen für Alter und Einstiegsgehalt der Absolventen.
Für das Alter existieren gleich zwei Modi (23 und 25), beim Einstiegsgehalt dagegen kein einziger, da jeder Wert nur einmal genannt wurde. Zudem ist die Aussagekraft des Modus beschränkt, weshalb Du immer prüfen solltest, ob Du nicht zusätzlich einen Median oder ein arithmetisches Mittel angeben kannst.
Neben dem Mittelwert sind Median und Modus wertvolle Hilfen, um deine Daten zu beschreiben. Von allen können zum Beispiel Datenverteilungen in SPSS beschrieben werden. Ob und wie sinnvoll Du sie berechnen kannst, ist von einer Reihe Faktoren abhängig. Neben dem Skalenniveau spielen auch die Existenz von Ausreißern sowie die Anzahl der Merkmalsausprägungen eine Rolle. Wenn möglich, solltest Du mehrere Maße berechnen, denn auch die Unterschiede zwischen Mittelwert, Median und Modus verraten etwas über deine Daten. Zu allen drei Lagemaßen bietet die Universität Kassel sogar interaktive Übungen an. Ein Statistik-Service kann dir helfen, falls du Probleme bei der Berechnung hast.