Hypothesentest: Du wirst im Laufe Deines Studiums und vielleicht auch darüber hinaus immer wieder Forschungsfragen aufstellen und untersuchen. Aber wie genau entscheidest Du am Ende, ob Deine Hypothese zutrifft oder nicht? Vorneweg: Den endgültigen Beweis kann und wird Dir die Statistik nicht liefern. Bis dahin bietet der Hypothesentest aber eine ausgezeichnete Alternative.
Was ist ein Hypothesentest?
Vermutlich hat jeder, der wissenschaftlich arbeitet, schon einmal von Hypothesen gehört. Der Duden definiert eine Hypothese als eine „[…]von Widersprüchen freie, aber zunächst unbewiesene Aussage, Annahme (von Gesetzlichkeiten oder Tatsachen) als Hilfsmittel für wissenschaftliche Erkenntnisse“. Zudem gilt sie als eines der wichtigsten Prinzipien für wissenschaftliches Arbeiten, dass wir nur solange von der Richtigkeit einer Hypothese ausgehen, bis wir sie falsifizieren können. Mit anderen Worten: Wir können unsere Hypothese niemals beweisen, sondern nur widerlegen.
Genau dieses Vorgehen machen wir uns auch in der Statistik zunutze, indem wir zwei Hypothesen konstruieren.
- H0: Die sogenannte Nullhypothese, die wir falsifizieren wollen
- H1: Die Alternative und meist unsere eigentliche Forschungshypothese
Angenommen, wir gehen davon aus, dass sich die Körpergröße von Männern und Frauen unterscheidet. In diesem Fall lautet die Nullhypothese: „Männer und Frauen sind gleich groß.“ Denn das ist ja genau das, was wir widerlegen möchten.
Wie bereits in der Einleitung erklärt, hilft Dir der Hypothesentest bei der Entscheidung für oder gegen Deine Forschungshypothese (bzw. aufgrund des Aufbaus eigentlich für oder gegen Deine Nullhypothese). Dabei ist die Zahl der möglichen statistischen Tests vielfältig, grundsätzlich folgen sie aber alle demselben Prinzip.
Vorbereitung auf den Hypothesentest
Zunächst erarbeitest Du Dir Deine Hypothesen. Achte schon zu Beginn darauf, dass Du diese mit der im letzten Abschnitt beschriebenen Form von Null- und Alternativhypothese ausdrücken kannst. Das erleichtert Dir später die Datenanalyse. Damit sind wir auch schon beim nächsten Punkt: den Daten.
Handelt es sich um eine Primärerhebung, solltest Du natürlich im Blick behalten, dass sich Deine Forschungsfrage mit den von Dir gesammelten statistischen Daten beantworten lässt. Ob Frauen und Männer verschieden groß sind, kannst Du nur durch einen Hypothesentest prüfen, wenn Du das Geschlecht Deiner Probanden kennst und ihre Größe ausreichend genau erhoben hast. Solltest Du Deine Daten über eine Sekundärerhebung beziehen, kann es sein, dass Du Deine Hypothesen anpassen musst, um sie zufriedenstellend zu beantworten.
Hypothesentest und Signifikanzniveau
Hypothesentests geben Dir nie 100%ige Sicherheit. Es besteht immer die Gefahr, Deine Nullhypothese abzulehnen, obwohl sie wahr ist, oder sie anzunehmen, auch wenn sie gar nicht stimmt. Siehe dazu auch Abbildung 1.
Abb 1: Fehler 1. und 2. Art
Den sogenannten Fehler 1. Art können wir jedoch durch das Signifikanzniveau beeinflussen. Dabei konstruieren wir unseren Hypothesentest so, dass die Wahrscheinlichkeit, den Fehler 1. Art zu begehen nicht unser zuvor festgelegtes Signifikanzniveau übersteigt (vgl. Fahrmeier et al., 2012).
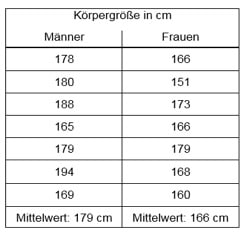
Kehren wir noch einmal zu unserem Beispiel zurück. Wir gehen davon aus, dass wir eine Stichprobe gezogen und Daten erhoben haben. Diese ergeben eine mittlere Körpergröße von 166 cm für Frauen und 179 cm für Männer (s. Tabelle 1).
Abb 2: Körpergröße Männer und Frauen
Im Prinzip fragen wir uns bei einem Hypothesentest nun Folgendes: „Wie wahrscheinlich ist es, einen Größenunterschied von mindestens 13 cm zu beobachten, wenn Männer und Frauen gleich groß sind?“ Liegt die Wahrscheinlichkeit dafür unter unserem Signifikanzniveau, lehnen wir H0 ab (und gehen damit das Risiko ein, den Fehler 1. Art zu begehen).
Welcher Hypothesentest ist der richtige?
Hast Du die in den letzten beiden Abschnitten beschriebenen Vorbereitungen getroffen, kannst Du einen Hypothesentest durchführen. Für welchen Test Du Dich dabei entscheiden solltest, ist von einer Vielzahl von Faktoren wie beispielsweise Deiner Forschungsfrage und dem Skalenniveau Deiner Daten abhängig.
Im Fall unseres Beispiels ist die uns interessierende Variable metrisch. Zudem wollen wir zwei Gruppen miteinander vergleichen. Hier bieten sich ein Gauß- oder t-Test an. Der Gauß-Test legt die Normalverteilung zugrunde und wird üblicherweise nur angewandt, wenn die Varianz der Grundgesamtheit bekannt ist. Müssen wir diese erst aus den Daten schätzen, verwenden wir hingegen den t-Test. Beide Tests sind für einseitige Hypothesen (z. B.: Männer sind größer als Frauen) oder zweiseitige Hypothesen (Männer und Frauen sind unterschiedlich groß) geeignet.
Aber was, wenn unsere Variable ordinalskaliert ist, oder wir keine Normalverteilung annehmen können? Dann sind oft parameterfreie Hypothesentests wie der Wilcoxon-Mann-Whitney-Test die Lösung.
Möchtest Du hingegen mehr als zwei Gruppen miteinander vergleichen, eignen sich eine ANOVA oder der Kruskal-Wallis-Test. Du merkst schon, die Auswahl ist groß. Bei der Universität Wien findest Du deshalb gängige Tests und ihre Anwendungsbereiche in einer Grafik zusammengestellt.
Wie interpretiere ich den Hypothesentest?
Am Ende reicht es natürlich nicht, den Test nur zu rechnen. Du musst seine Ergebnisse korrekt interpretieren. Während Du beim händischen Rechnen eines Gauß- oder t-Tests üblicherweise eine Teststatistik bestimmst, um sie anschließend mit dem Referenzwert zu vergleichen, geben Dir Statistikprogramme wie das R Programm oder die SPSS Software sogenannte p-Werte aus.
Dementsprechend werden diese oft in der Forschungsliteratur angegeben. Die Bedeutung des p-Werts haben wir im Grunde bereits besprochen. Es ist jene Wahrscheinlichkeit, deren Grenzwert das Signifikanzniveau darstellt. Wir können unsere auf unser Beispiel gemünzte Aussage nun also verallgemeinern: „Mit welcher Wahrscheinlichkeit beobachte ich Daten, die mindestens so stark für meine Alternativhypothese sprechen wie die vorliegenden, wenn eigentlich die Nullhypothese gilt?“.
Häufig wird bei einem p-Wert von unter 0,05 von einem „signifikanten Ergebnis“ gesprochen. Das bedeutet nicht, dass H1 bewiesen ist. Wir halten eine Irrtumswahrscheinlichkeit von 5% nur für klein genug, um das Risiko einzugehen H0 abzulehnen. Seit einigen Jahren wird jedoch argumentiert, dass zur besseren Reproduzierbarkeit von Studienergebnissen strengere Signifikanzniveaus angelegt werden sollten (vgl. Johnson, 2013).
Der Hypothesentest ist ein wichtiges Hilfsmittel zur Prüfung von Forschungsfragen. Um gute Ergebnisse zu erhalten, sollte ihre Konstruktion bereits bei der Erarbeitung der Fragestellung und der Datenerhebung beachtet werden. Wenn Du Dir nicht sicher bist, kannst Du auch auf eine Statistik-Beratung zurückgreifen, oder mit Statistik Nachhilfe Deine Leistung langfristig verbessern.
Letztendlich gilt: Welcher Hypothesentest für Dich der richtige ist, hängt von einer Vielzahl von Faktoren ab, aber sein Grundprinzip und seine Interpretation bleiben nahezu identisch.
Literatur
Fahrmeir, Ludwig/Heumann, Christian/Künstler, Rita/Pigeot, Iris/Tutz, Gerhard (2012): Statistik: Der Weg zur Datenanalyse, 7. Auflage Berlin.
Johnson, Valen E. (2013): Revised standards for statistical evidence, in: Proceedings of the National Academy of Sciences of the United States of America 110 (48), S. 19313–19317.