Statistische Regression beschreibt den Zusammenhang zwischen zwei oder mehr Variablen. Das Ziel ist es, eine Vorhersage treffen zu können. Wenn Du Informationen über eine von zwei Variablen hast, liefert Dir die Regression eine Schätzung, wie die Ausprägung der anderen Variablen im Durchschnitt zu erwarten ist. Dieser Zusammenhang ist meist linear, das heißt, er kann durch eine Gerade beschrieben werden. Im folgenden Artikel beschreiben wir, wie man eine Regression berechnet, welche Arten von Regressionen es gibt und wie man Regressionsanalysen interpretieren kann, zum Beispiel mit R Outputs.
Was ist eine statistische Regression?
Um eine statistische Regression zu berechnen, benötigst Du mindestens zwei Variablen. Im einfachsten Fall sind beide Variablen metrisch, es gibt aber auch die Möglichkeit, eine Regression mit kategorialen oder ordinal skalierten Variablen zu berechnen. Hilfreiche Hinweise hierzu findest Du unter Skalenniveaus in SPSS. Das Ergebnis der Rechnung sagt Dir, wie stark der Zusammenhang ist und ob er statistisch signifikant, also gegen den Zufall abgesichert ist.
Außerdem erfährst Du die Art und die Richtung des Zusammenhanges: Ein positiver Zusammenhang beschreibt die Form “je mehr desto mehr”, ein negativer Zusammenhang erkennst Du am negativen Vorzeichen des Regressionskoeffizienten. Er beschreibt eine “je mehr desto weniger“-Beziehung. Hier kann die Parallele zu Korrelationen in SPSS klar erkannt werden.
Wenn ein signifikanter Zusammenhang vorliegt, kannst Du aus der Information über die eine Variable auf die Ausprägung der anderen schließen. Angenommen, Deine Variablen sind „Sonnenstunden“ und „Anzahl der Blüten in Deinen Sonnenblumen“. Du möchtest anhand der Anzahl der Sonnenstunden, die Du mithilfe der Wettervorhersage schätzt, ausrechnen, wie viele Blüten die Sonnenblumen etwa entwickeln werden.
Die Anzahl der Sonnenstunden ist im obigen Beispiel der Prädiktor, damit ist die vorhersagende Variable gemeint. Sie wird manchmal auch als Regressor bezeichnet. Die Anzahl der Blüten ist die Kriteriumsvariable. Sie heißt so, weil Du über diese Variable eine Vorhersage treffen willst.
Statistische Regression: Welche Arten gibt es?
Bei einer einfachen linearen Regression gehen genau zwei Variablen in die Analyse ein. Sie sind beide metrisch und der angenommene Zusammenhang ist linear. Es gibt auch andere Formen der statistischen Regression, zum Beispiel die multiple Regression, bei der mehrere Prädiktoren aufgenommen werden. Das ist oft sinnvoll, da man die Kriteriumsvariable in vielen Fällen mit nur einer Variable nicht gut vorhersagen kann.
Des Weiteren ist es auch möglich, kategoriale Variablen als Prädiktorvariablen aufzunehmen. Dazu bedarf es einer Kodierung (z.B. die Dummy- oder Effektkodierung). Ist die Kriteriumsvariable nominalskaliert, kann man eine logistische Regression berechnen. Zudem gibt es auch die Möglichkeit, nichtlineare, also etwa quadratische Effekte, zu berücksichtigen.
Jetzt haben wir viel über verschiedene Arten von Zusammenhängen bzw. über die Frage, ob ein Zusammenhang linear ist, gesprochen. Was ist damit gemeint? Inhaltlich bedeutet linear, dass eine Veränderung der einen Variable mit der gleichen Veränderung in der anderen Variablen einhergeht.
Im Beispiel mit den Sonnenblumen geht das Modell also davon aus, dass mit jeder weiteren Sonnenstunde, die Anzahl der zu erwartenden Blüten um einen bestimmten Wert steigt. Nehmen wir an, dass dieser Wert 0,3 ist. Das bedeutet, dass Sonnenblumen, die eine Sonnenstunde mehr genossen haben als andere, im Durchschnitt 0,3 mehr Blüten haben. Und zwar ist diese Steigerung unabhängig davon, ob es eine Steigerung von 13 auf 14 Stunden Sonnenschein gab oder von 2 auf 3 Stunden.
Natürlich sind nicht alle Zusammenhänge linear. Zum Beispiel kann man davon ausgehen, dass Menschen mit mehr Freunden zufriedener sind als Menschen mit weniger Freunden. Aber dieser Effekt dürfte nicht linear sein: Eine Steigerung von 3 auf 4 Freunde hat vermutlich einen größeren Einfluss auf die Zufriedenheit als eine Steigerung von 80 auf 81. Zu diesem Thema kannst du auch einen Statistik-Service befragen.
Statistische Regression mit SPSS
Verschiedene Statistikprogramme übernehmen die Berechnung für eine statistische Regression, sodass man meist mit wenigen Klicks oder einem kurzen Befehl das gewünschte Ergebnis erzielen kann. Um die Outputs zu verstehen, ist es hilfreich, eine grobe Vorstellung von dem zugrundeliegenden Algorithmus zu haben.
Die Idee der Regression basiert auf der Varianzzerlegung. Das heißt, dass man die Varianz beider Variablen aufteilt in eine gemeinsame und eine geteilte Varianz. Je mehr gemeinsame Varianz es gibt, desto besser kann man mithilfe der Prädiktorvariablen das Kriterium vorhersagen. Im einfachsten Fall der einfachen linearen Regression sieht die Formel für die statistische Regression so aus:
Kriterium = Konstante + Prädiktor*Koeffizient.
Wie interpretiert man die Outputs?
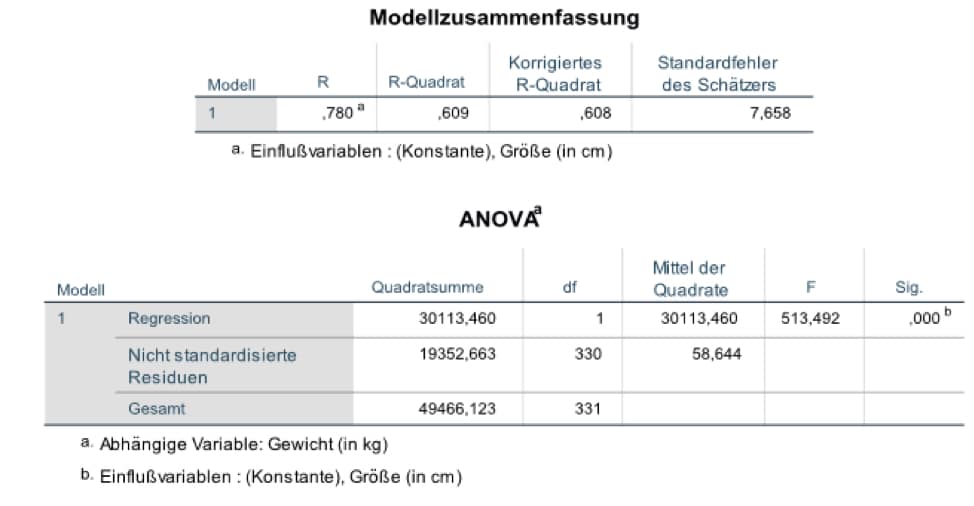
Die Homepage der Uni Trier bietet einen Überblick über die statistische Regression in SPSS. Die SPSS Software liefert drei Ergebnistabellen für eine lineare Regression. Die erste ist eine Modellzusammenfassung. Dort findest Du den Zusammenhang (die Korrelation) zwischen den untersuchten Variablen in der Spalte „R“. R-Quadrat ist der Determinationskoeffizient. Dieser gibt an, wie viel Varianz die statistische Regression erklären kann. Zudem findest Du noch einen korrigierten Determinationskoeffizienten, der die Anzahl der Prädiktoren und der Versuchseinheiten berücksichtigt, und den Standardschätzfehler.
Als zweite Tabelle erhältst Du eine Übersicht mit dem Titel „ANOVA“. Dort ist die Varianzzerlegung, oder auch Quadratsummenzerlegung, beschrieben. ANOVAS lassen sich besonders gut mit dem R Programm berechnen. Die wichtigste Information in dieser Tabelle steht in der letzten Spalte unter „Sig.“, das steht für Signifikanz. Dort kannst Du ablesen, ob das gesamte Modell statistisch signifikant ist. Wenn das nicht der Fall sein würde, ist der gefundene Zusammenhang nicht größer als die normale Zufallsschwankungen. In diesem Fall solltest Du die statistische Regression nicht oder nur mit Vorsicht interpretieren. Hilfe kann dir außerdem ein Datenanalyse Service geben.
Abbildung 1: Die ersten beiden Output-Tabellen mit globalen Informationen für statistische Regression
Die Regressionsgleichung aufstellen
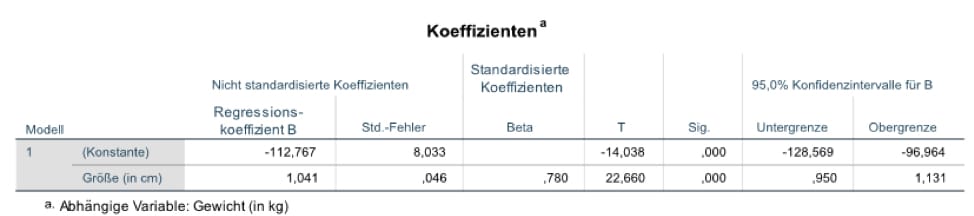
Die dritte Tabelle gibt Details zu der Vorhersage an. Das Beispiel betrachtet den Zusammenhang zwischen Körpergröße und Körpergewicht. Du kannst aus der Tabelle die obige Formel für Deine Daten ableiten: Du findest den Wert der Konstanten. Diese gibt den zu erwartenden Wert an, wenn der Prädiktor gleich null ist (im Fall der Körpergröße ist das offenbar kein sinnvoller Wert).
In der Tabelle findest Du auch den Regressionskoeffizienten, in diesem Beispiel ca. 1,04. Der Koeffizient ist die Steigung der Regressionsgeraden. Das bedeutet, dass mit jedem Zentimeter Körpergröße das durchschnittliche Gewicht um 1,04 kg steigt. Das Vorzeichen des Koeffizienten gibt Aufschluss über die Richtung des Zusammenhangs. Ist es positiv, gilt, je größer, desto größer wie in unserem Beispiel. Ist es negativ, gilt, je größer, desto kleiner. Das kannst Du Dir mit dem Beispiel „je mehr ich mich vorbereite, desto weniger Angst habe ich“ veranschaulichen. Dann gibt es noch den standardisierten Koeffizienten. Der ist dazu nützlich, um Vergleiche zwischen verschiedenen Modellen anzustellen. Schließlich gibt es für jeden Koeffizienten einen Signifikanztest und ein Konfidenzintervall.
Abbildung 2: Die dritte Output-Tabelle mit Details zum Beitrag der einzelnen Prädiktoren für die statistische Regression
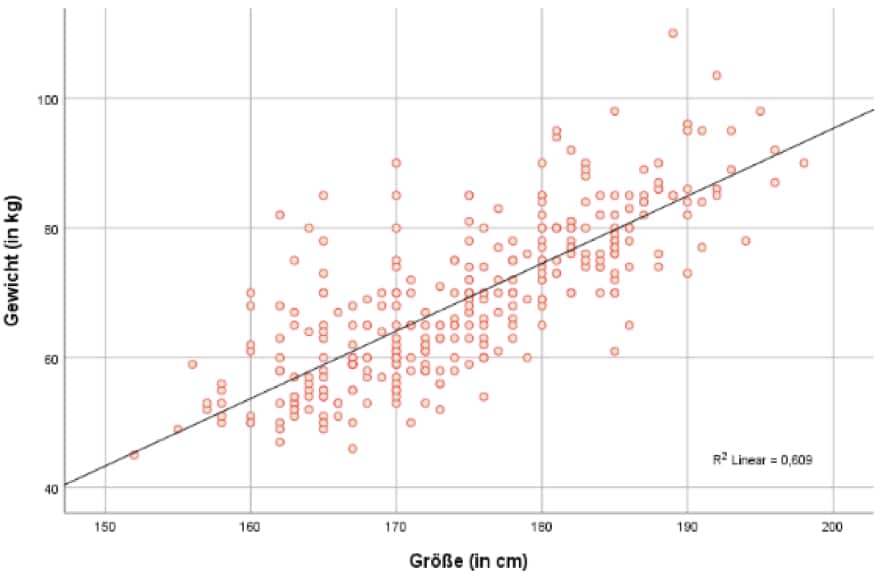
Abbildung 3: Scatterplot mit einer Regressionslinie zur Visualisierung der Streuung der Daten und der Stärke des Zusammenhangs
Eine detaillierte Beschreibung für alle Informationen im SPSS-Output kannst Du auf den Seiten der Freien Uni Berlin finden.
Die Regressionsanalyse ist ein mächtiges und nützliches Mittel in der Statistik. Es gibt viele verschiedene Arten von Regressionen, auf die man zurückgreifen kann. Das ermöglicht es, für sehr verschiedene Daten eine statistische Regression zu berechnen. Mithilfe von Statistikprogrammen wie SPSS oder R kannst Du mit wenig Aufwand selbst Regressionen berechnen, wenn du dabei eine Unterstützung brauchst, wende dich an eine Statistik Beratung.