Clusteranalyse SPSS: Die Clusteranalyse hat zum Ziel, die Fälle Deines Datensatzes anhand der Ausprägungen der vorliegenden Variablen in Gruppen aufzuteilen. Dabei sollen die Gruppen in sich möglichst homogen sein, zwischen den Gruppen aber soll möglichst viel Unterschied bestehen.
Ein typischer Einsatzbereich ist die Marktsegmentierung in der Marktforschung, um etwa potenzielle Kunden in Käufertypen aufzuteilen. Diese können dann mit dem entsprechenden Marketinginstrumentarium optimal angesprochen werden. Zudem kannst du mit diesem Verfahren statistische Daten für deine Bachelorarbeit oder Masterarbeit aus Online-Umfragen gewinnen.
Als erstes musst Du festlegen, wie die Distanz zwischen den Objekten berechnet werden soll. Dabei ist vor allem dem Skalenniveau der verschiedenen Merkmale Rechnung zu tragen. Wenn du hierbei und im weiteren Verlauf Hilfe benötigst, dann bietet sich Statistik Nachhilfe an.
Dann entscheidest Du Dich, welchen Typ der Clusteranalyse Du durchführen möchtest und wählst dementsprechend die passende Menüfolge in SPSS aus. Einige hilfreiche Hinweise und Erklärungen dazu findest Du beispielsweise bei der Universität Duisburg-Essen.
Clusteranalyse mit SPSS: Bestimmung von Ähnlichkeitsmaßen
Falls Du ausschließlich metrisch skalierte Merkmale (Variablen) vorliegen hast, ist die Bestimmung der Ähnlichkeits-bzw. Distanzmaße sehr einfach. Du kannst dann die euklidische Distanz zwischen beiden Objekten berechnen. Im Fall von zwei beobachteten Merkmalen kannst Du Dir vorstellen, dass die beobachteten Fälle in ein zweidimensionales Punktediagramm eingezeichnet wären. Die euklidische Distanz ist dann einfach der Abstand zwischen zwei Punkten.
Hast Du dagegen ordinal oder sogar nominalskalierte Merkmale, so kannst Du die Abstände zwischen den Ausprägungen nicht messen. Es gibt eine Reihe von Ansätzen (vgl. Backhaus et al. 2013), wie Du bei nicht-metrischen Merkmalen vorgehen kannst. Du könntest beispielsweise bei allen nominalskalierten Merkmalen bezüglich eines Objektpaares zählen, in wie vielen Fällen die gleiche Ausprägung vorliegt. Anschließend dividierst Du dann diese Anzahl durch die Gesamtzahl der betrachteten Merkmale.
Sodann kann man die nach Skalenniveau gebildeten Distanzmaße in ein Gesamtmaß zusammenführen.
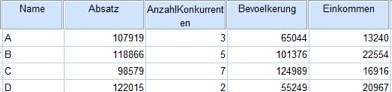
Im Folgenden gehen wir ausschließlich von metrischen Daten aus. Dein Datensatz besteht aus Merkmalen (Variablen), die für 33 Restaurants in Hessen erhoben wurden:
Abb. 1: Merkmale von Restaurants
Die hierarchische Clusteranalyse mit SPSS
Hier bildet jeder Fall zu Beginn ein eigenes Cluster. Du berechnest die Distanzen zwischen allen Clustern und verbindest die beiden miteinander, deren Distanz am geringsten ist. Für das verschmolzene Cluster ermittelst Du anschließend das neue Zentrum und beginnst von vorn. So kannst Du in jedem Schritt des Verfahrens die Anzahl der Cluster um eins reduzieren.
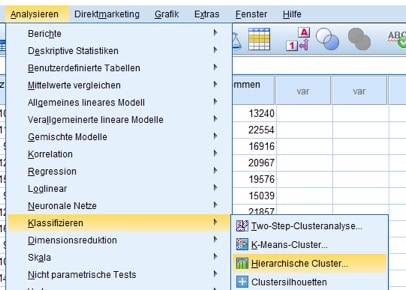
Für die Durchführung mit der SPSS Software wählst Du die Menüfolge “Analysieren/Klassifizieren/Hierarchische Cluster“.
Abb. 2: Menüfolge für die hierarchische Clusteranalyse SPSS
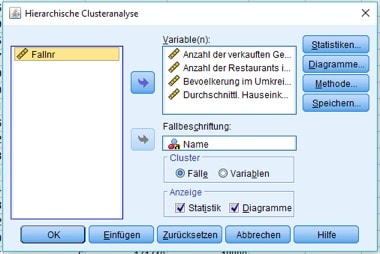
Es öffnet sich eine Dialogbox, in die Du die zu berücksichtigenden Merkmale einträgst.
Abb. 3: Dialogbox der hierarchischen Clusteranalyse mit SPSS
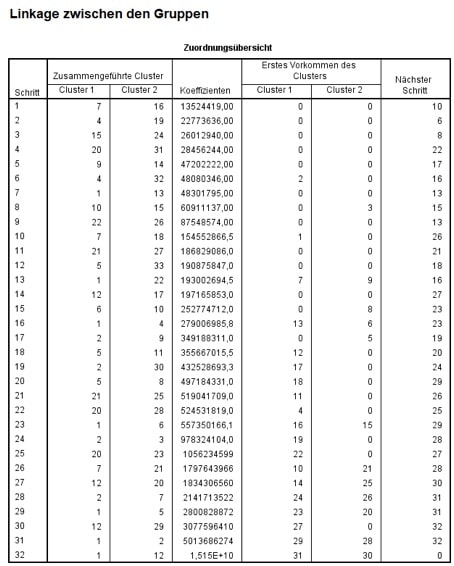
Klicken auf OK ergibt den folgenden Output.
Abb. 4: SPSS-Output der hierarchischen Clusteranalyse in SPSS
Du kannst hier genau nachvollziehen, in welchem Schritt des Verfahrens welche Cluster miteinander verschmolzen wurden. Das neue Cluster erhält dann die Bezeichnung des in der ersten Spalte aufgeführten. Am Ende liegen schließlich alle Fälle in einem gemeinsamen Cluster, hier in dem mit der Nummer 1.
Den jeweiligen Wert in der Spalte „Koeffizienten“ kannst Du als Maß für die Uneinheitlichkeit innerhalb der Cluster interpretieren. Je weniger Cluster es gibt, desto unterschiedlichere Fälle liegen natürlich innerhalb eines Clusters.
Die Verfahren sind nicht für große Fallzahlen geeignet, aber es können Variablen aller Skalenniveaus berücksichtigt werden. Eine Statistik Beratung kann in jedem Fall Aufschluss darüber geben, welches Verfahren sich am besten eignet.
K-Means-Clusteranalyse in SPSS
Die K-Means-Clusteranalyse ist ausschließlich bei metrisch-skalierten Merkmalen anzuwenden, da sie die euklidische Distanz als Maß für die Unähnlichkeit zugrunde legt. Aber sie kann auch sehr große Datensätze verarbeiten.
Du gibst zu Beginn vor, in wie viele k Cluster Du die beobachteten Fälle aufteilen möchtest, nimmst k beliebige Fälle als vorläufige Clusterzentren heraus und teilst die übrigen entsprechend ihrer Distanz den k Clustern zu. Nach Berechnung der resultierenden Clusterzentren erfolgt die erneute Verteilung aller Fälle auf diese Cluster (vgl. dazu auch Janssen/Laatz, 2017).
Es läuft ein iteratives Prozessverfahren, das so lange wiederholt wird, bis die durch Neuzuordnung erzielte Verbesserung eine vorher gewählte Größe unterschreitet.
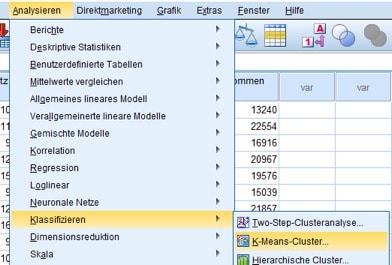
In SPSS wählst Du die Menüfolge „Analysieren/Klassifizieren/K-Means-Cluster“.
Abb. 5: Menüfolge für die K-Means-Clusteranalyse mit SPSS
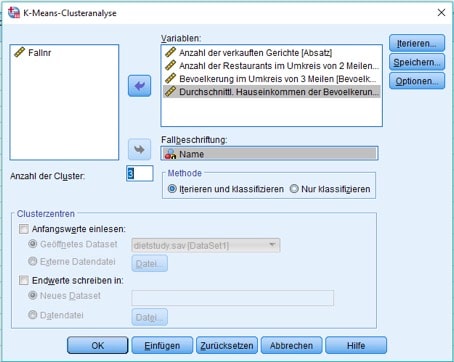
Klicken auf „OK“ bringt Dich in eine Dialogbox, in der Du die zu berücksichtigenden Variablen sowie die Fallbeschriftung eingeben kannst. Außerdem gibst Du hier an, in wie viele Cluster Du diese aufteilen möchtest. In diesem Fall werden 3 Cluster gewünscht.
Abb. 6: Dialogbox für die K-Means-Clusteranalyse
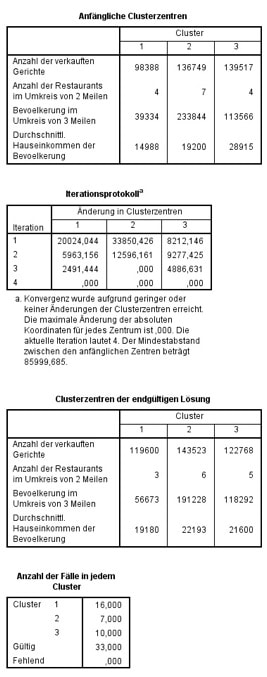
Du erhältst Deinen umfangreichen SPSS-Output. Zunächst werden die ursprünglichen zufälligen Clusterzentren aufgeführt. Sodann siehst Du die Anzahl der Iterationen, die endgültigen Clusterzentren und die Anzahl der jeweils enthaltenen Fälle. Um die Richtigkeit deines Outputs zu gewährleisten, empfiehlt es sich in jedem Fall auf fundiertes Fachwissen von Experten zurückzugreifen und von dem Datenanalyse Service inklusive Beratung mit SPSS, R, STATA zu profitieren.
Abb. 7: SPSS-Output für die K-Means-Clusteranalyse.
Two-Step-Clusteranalyse mit SPSS
Diese Verfahren vereinen die Vorteile und Vorgehensweisen der beiden vorherigen Verfahren. Das heißt, sie sind auf Datensätze aller Skalenniveaus anwendbar und es können große Fallzahlen bearbeitet werden. Der Statistik Service für Studenten und Unternehmen unterstützt dich bei der Wahl der richtigen Herangehensweise.
Im ersten Schritt werden die Fälle mit einem speziellen Distanzmaß so in Cluster aufgeteilt, dass die Unähnlichkeit innerhalb eines Clusters ein vorher angegebenes Maß nicht übersteigt. Passt ein Fall demnach nicht zu einem schon vorhandenen Cluster, wird ein neues eröffnet. Wie viele Cluster dafür schließlich erforderlich sind, bestimmt das Verfahren.
Im zweiten Schritt werden dann die eben bestimmten Cluster einer hierarchischen Clusteranalyse unterzogen.
Die Verfahren der Clusteranalyse dienen dazu, die Fälle Deines Datensatzes in Gruppen so aufzuteilen, dass die Elemente innerhalb einer solchen Gruppe möglichst ähnlich sind. Welche Verfahrensgruppe Du anwendest, hängt zum einen vom Skalenniveau Deines Datensatzes und zum anderen von der Anzahl der Fälle ab. In jedem Fall liefert Dir SPSS das Analyseergebnis. Statistische Ergebnisse formulieren wäre dann der finale Punkt, der dein Projekt abrundet.
Literatur
Janssen, Jürgen/Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage, Berlin.
Backhaus, Klaus/Erichson, Bernd/Plinke, Wulff/Schuchard-Ficher, Christiane/Weiber, Rolf (2013): Multivariate Analysemethoden. Eine anwendungsorientierte Einführung, 5. revidierte Auflage, Berlin, Heidelberg