Die bivariate Statistik im Allgemeinen analysiert zwei Variablen gemeinsam. Du kannst daher über die univariate Statistik hinaus zum einen Zusammenhänge zwischen je zwei Variablen untersuchen. Zum anderen kannst Du aber auch eventuell bestehende Abhängigkeiten zwischen ihnen ermitteln. Bei der Auswahl der geeigneten Methode ist immer das Skalenniveau in SPSS Deiner Daten ganz wichtig. Hier findest du eine detailliertere Übersicht über die Methoden der bivariaten Statistik. Mit der SPSS Software erhältst Du Deine Ergebnisse dann wieder wie gewohnt schnell und unkompliziert.
Bivariate Statistik: Übersicht über Skalenniveaus
Schauen wir uns im Zusammenhang mit der bivarianten Statistik die möglichen Skalenniveaus an. In der Statistik kannst Du entsprechend drei verschiedene Skalenniveaus unterscheiden (vgl. Benninghaus, 2013):
- Nominalskala: Ein Merkmal ist dann nominalskaliert, wenn Du nur unterschiedliche Ausprägungen eines Merkmals feststellen kannst. Sie lassen sich aber nicht in eine Rangfolge bringen und noch weniger kannst Du Unterschiede zwischen den Kategorien messen. Nominalskalierte Merkmale sind beispielsweise Geschlecht, Studienfach, Farbe usw.
- Ordinalskala: Ein Merkmal heißt ordinalskaliert, wenn sich seine Ausprägungen zwar in eine Rangfolge bringen lassen, Du aber die Abstände zwischen den Ausprägungen nicht messen kannst. Das ist beispielsweise die Platzierung von Sportlern bei Wettkämpfen.
- Metrische Skala: Ein Merkmal heißt metrisch skaliert, wenn die von Dir erhobenen Daten als numerische Werte vorliegen, mit denen Du auch Rechenoperationen durchführen kannst. Ein Proband im Alter von 60 Jahren ist folglich dreimal so alt wie einer im Alter von 20 Jahren, und genau 10 Jahre älter als einer von 50 Jahren.
Von der Nominalskala über die Ordinalskala bis hin zur metrischen Skala nimmt der Informationsgehalt der Datenverteilung in SPSS zu. Umso differenziertere und sicherere Aussagen gibt Dir dann auch die bivariate Statistik. Wenn Dich in diesem Bereich Unsicherheiten plagen, dann ist die Statistik Nachhilfe ratsam.
Vorstellung zweier Datensätze für die bivariate Statistik
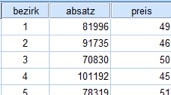
Zum einen hast Du für deine Datenanalyse in SPSS einen metrischen Datensatz gegeben: Um beispielsweise die Wirkung von Preisänderungen auf Deinen Absatz von Weinflaschen zu untersuchen, hast Du gerade eine kleine Stichprobe erhoben. Für 16 Bezirke wurden jeweils die Absatzmenge in Flaschen und der geforderte Verkaufspreis notiert:
Abb. 1:
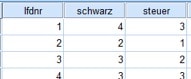
In einer anderen Erhebung für die bivariate Statistik befragst Du die Probanden, wie sie Schwarzfahren bzw. Steuerbetrug auf einer Skala von 1 bis 4 beurteilen. Dabei bedeutet 1: „sehr schlimm“ bis hin zu 4: „weniger schlimm“. Hier hast Du demnach einen ordinalskalierten Datensatz gegeben.
Abb. 2: Ordinalskalierter Datensatz
Gemeinsame Häufigkeitsverteilung
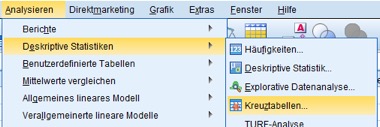
Daraus kannst Du nun die zweidimensionalen Häufigkeiten mit Hilfe der SPSS Syntax berechnen lassen, hier für den zweiten Datensatz beispielsweise. Nach dem SPSS Daten Importieren kann es auch schon losgehen. Du erhältst diese bivariate Statistik durch die Menüfolge: Analysieren/Deskriptive Statistiken/Kreuztabellen:
Abb. 3: Menüfolgen für die zweidimensionalen Häufigkeiten
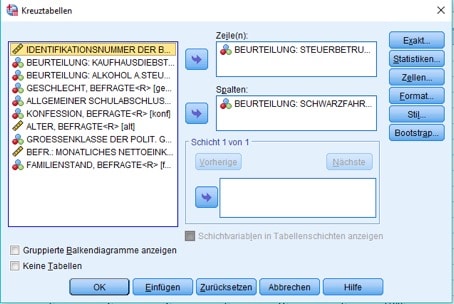
Danach gibst Du an, welche Variablen Du zeilen- bzw. spaltenweise angeordnet haben möchtest.
Abb. 4: Dialogbox Kreuztabellen
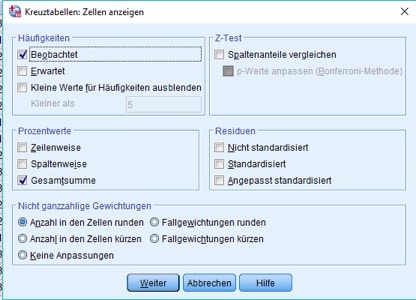
Durch Anklicken von „Zellen“ bestimmst Du im nächsten Schritt ganz genau, welche Häufigkeiten berechnet werden sollen:
Abb. 5: Dialogbox Zellen
Hier interessieren im Moment vor allem die Prozentwerte, beziehungsweise genauer gesagt die Prozentwerte, bezogen auf die Gesamtsumme. Du erhältst dadurch die relativen Häufigkeiten, mit der beispielsweise ein Proband es sowohl für ziemlich schlimm ansieht, Steuerbetrug zu betreiben, als auch Schwarzfahrer zu sein.
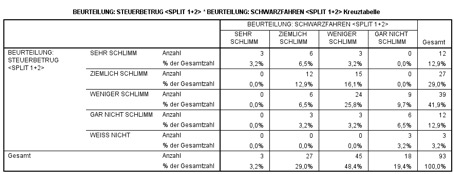
Klickst Du erst auf weiter und dann auf OK, so erhältst Du Dein Ergebnis zu:
Abb. 6: Kreuztabelle mit absoluten und relativen Häufigkeiten.
Im Fall von metrischen Merkmalen bietet es sich für eine Kreuztabelle natürlich an, die Werte zu gruppieren, um überschaubare Gruppenzahlen zu erhalten (Vgl. dazu auch Eckstein, 2016).
Zusammenhangmaße für die bivariate Statistik
Du siehst an den deutlich erhöhten Häufigkeiten auf der Hauptdiagonalen der Tabelle in Abbildung 6, dass, wie man eigentlich auch erwarten kann, ein Zusammenhang zwischen den beiden Beurteilungen zu bestehen scheint: Wer einen Steuerbetrug für verwerflich hält, findet auch Schwarzfahren schlimm und umgekehrt.
Um ihn zu messen und auf Signifikanz zu testen, umfasst die bivariate Statistik je nach Skalenniveau geeignete Zusammenhangmaße.
Metrische Korrelationskoeffizienten
Du kannst SPSS für Deinen metrischen Datensatz zunächst das klassische Zusammenhangmaß für die bivariate Statistik berechnen lassen, nämlich Pearsons Korrelationskoeffizient (Vergleiche auch die Ausführungen der Kent State University).
Dieser berechnet die Kovarianz zwischen beiden Merkmalen und normiert sie anschließend auf den Bereich zwischen Null und Eins. Sein Wert gibt Dir dann den prozentualen Anteil der Streuung an, der durch einen linearen Zusammenhang zwischen beiden Merkmalen erklärt wird. Die Software unterrichtet Dich über eine Korrelation in SPSS. Alternativ bietet sich Dir natürlich der Statistik-Service.
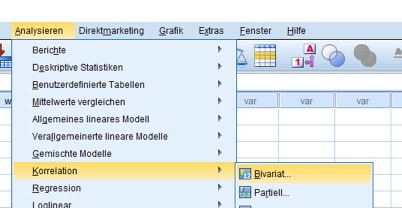
In SPSS lautet Deine Menüfolge: Analysieren/Korrelation/Bivariat.
Abb. 7: Menüwahl für Pearsons Korrelationskoeffizient
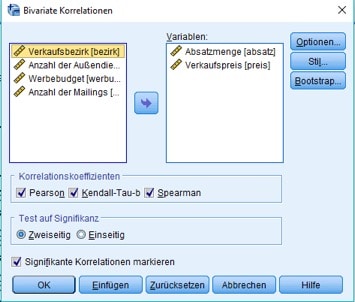
In der sich dann öffnenden Dialogbox wählst Du die Dich jetzt interessierenden Variablen einzeln an. Unten im Fenster bestimmst Du darüber hinaus, welche der Koeffizienten SPSS berechnen soll.
Hier wurden alle Koeffizienten ausgewählt.
Abb. 8: Dialogbox für die Berechnung von Korrelationskoeffizienten
Klicken auf „OK“ ergibt als ersten Output:
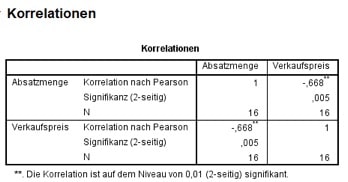
Abb. 9: SPSS-Output zur Korrelation.
Ein Korrelationskoeffizient von Null lässt auf einen fehlenden Zusammenhang schließen. Ein Wert von (minus) eins bedeutet dagegen einen sehr starken positiven (negativen) Zusammenhang zwischen den Merkmalen. Wie zu erwarten war, zeigt der hier berechnete Wert von -0,668 entsprechend an: Wenn der Preis steigt, sinkt die Nachfrage.
Mithilfe des unter „Signifikanz (2-seitig)“ angegebenen p-Wertes kannst Du für diese bivariate Statistik testen, ob der beobachtete Zusammenhang signifikant von Null verschieden ist: Bevor du die statistische Analyse durchführst, bestimmst Du dazu die gewünschte Irrtumswahrscheinlichkeit, meistens wählt man 0,05. Nur wenn der p-Wert kleiner als Deine Irrtumswahrscheinlichkeit ist, ist der Zusammenhang signifikant.
Korrelationskoeffizienten für ordinalskalierte Merkmale
Für ordinalskalierte statistische Daten ist der Pearson´schen Koeffizienten ungeeignet. Du wählst dann oft das Spearman-Rho aus, bei dem, grob gesagt, der Korrelationskoeffizient der Rangwerte ermittelt wird.
Kendalls Tau beruht dagegen auf einem ganz anderen Konzept und ist größenmäßig nicht mit den anderen Maßen vergleichbar.
Der zweite Output aus Deiner Wahl in Abb. 8 sind demzufolge diese beiden Koeffizienten:
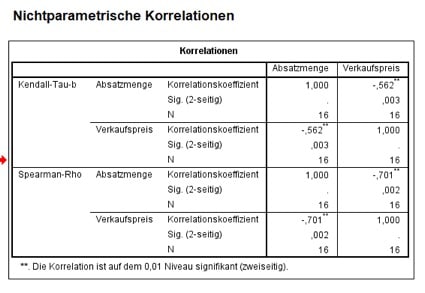
Abb. 10: SPSS-Output zu nichtparametrischen Korrelationen
Auch hiermit erhältst Du also wie im metrischen Fall einen signifikanten negativen Zusammenhang.
Test des Zusammenhangs für nominalskalierte Merkmale
Im nominalen Fall lässt sich keine Korrelation berechnen. Immerhin kannst Du mithilfe der Kreuztabellen einen Chi-Quadrat-Test dazu durchführen, ob überhaupt ein Zusammenhang zwischen den Variablen besteht.
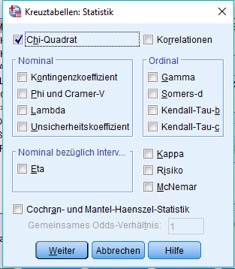
Klickst Du oben in der Abbildung 4 auf „Statistiken“ , so kannst Du beispielsweise Chi-Quadrat auswählen:
Abb. 11: SPSS-Dialogbox für Kreuztabellen
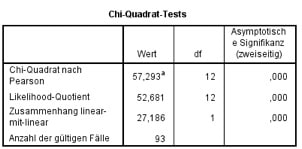
Zusätzlich zur Kreuztabelle erhältst Du damit ein signifikantes Ergebnis für den Chi-Quadrat-Test auf Unabhängigkeit:
Abb. 12: SPSS-Output des Chi-Quadrat-Tests
Analysemethoden, die die Art der Abhängigkeit weiter untersuchen, ergänzen die bivariate Statistik. Dabei wählst Du wie immer entsprechend dem Skalenniveau Deiner Variablen aus.
Die bivariate Statistik analysiert also über die isolierte Betrachtung der einzelnen Variablen hinaus deren Zusammenhänge und Abhängigkeiten. Der Datenanalyse Service kann Dir behilflich sein, komplexe Zusammenhänge zu verknüpfen.
Literatur
Benninghaus, Hans (2013): Deskriptive Statistik: Eine Einführung für Sozialwissenschaftler, 9. Auflage, Heidelberg.
Eckstein, Peter P. (2016): Angewandte Statistik mit SPSS, 8. Auflage, Berlin.