Die inferenzielle Statistik, auch induktive oder einfach schließende Statistik genannt, trifft Aussagen über die Daten Deiner Stichprobe hinaus. Sie schließt dazu mit Methoden der Wahrscheinlichkeitstheorie von der Stichprobe auf die unbekannte Grundgesamtheit und nimmt daran ein Hypothesentest vor. Damit ist sie immer dann anwendbar, wenn es zu aufwendig oder teuer wäre, alle Daten der Grundgesamtheit zu erheben und dann deren deskriptive Statistik zu berechnen.
Bis 1987 etwa wurde beispielsweise in Deutschland in regelmäßigen Abständen eine Volksbefragung durchgeführt, um die Informationen über die Bevölkerung zu aktualisieren. Nicht nur aus Gründen des Datenschutzes wurde dies abgeschafft. Es ist natürlich außerdem wesentlich einfacher und kostengünstiger, nur eine repräsentative Stichprobe der Bevölkerung zu erheben. Ist diese aber sorgfältig ausgewählt und erhoben, ist, wie viele meinen, der Schluss von der Stichprobe auf die Gesamtheit durch die inferenzielle Statistik auch genauer. Unklarheiten kann in diesem Fall die Statistik Nachhilfe beseitigen.
Zunächst kannst Du die inferenzielle Statistik grob in drei Bereiche einteilen.
Stichprobentheorie
Die Stichprobentheorie beschäftigt sich mit der optimalen Auswahl der Stichprobe und hat insofern nichts mit der SPSS-Analyse zu tun. Dazu gehören zunächst theoretische Überlegungen, denn die Stichprobe sollte verschiedenen Aspekten genügen:
- Sie sollte repräsentativ sein, d.h. also, von der Struktur her wie die Grundgesamtheit aufgebaut sein.
- Die Stichprobe sollte des Weiteren zum einen ausreichend groß sein, um Aussagen mit einer gewünschten Sicherheit treffen zu können.
- Zum anderen sollte sie möglichst klein sein, um Aufwand und Kosten so gering wie möglich zu halten.
Darüber hinaus liefert die Stichprobentheorie für die inferenzielle Statistik Auswahlverfahren für die Stichprobenelemente und Methoden zur Bestimmung der optimalen Stichprobengröße. Eine umfangreichere Beschreibung findest Du beispielsweise im Kompakt-Lexikon Wirtschaftsmathematik und Statistik (2013).
Schätztheorie
Mit „Schätzen“ bezeichnet man zunächst das Schließen von der Stichprobe auf die unbekannten Parameter der Grundgesamtheit und mit „Schätztheorie“ die dazu entwickelten Methoden. Die Berechnungen hierzu lassen sich sehr einfach mit der SPSS Software durchführen.
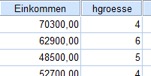
Stell Dir vor, Du hast in einer Stichprobe unter anderem das Jahreseinkommen und die Haushaltsgröße von Besuchern eines Marktes erhoben und möchtest daraus die entsprechenden Werte für die Bewohner der Stadt schätzen. Deine Stichprobe, bei der eine repräsentative Auswahl hier einfach unterstellt wird, sieht beispielsweise so aus:
Abb. 1: Stichprobenerhebung von Einkommen und Haushaltsgröße
Inferenzielle Statistik: Punktschätzung der Parameter
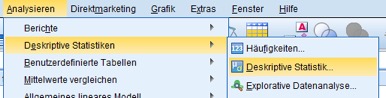
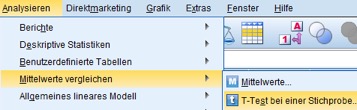
Nach dem SPSS Daten Importieren lässt Du SPSS nun aus diesen Daten den Mittelwert und Standardabweichung der Grundgesamtheit schätzen. Dazu verwendest Du am einfachsten die Menüfolge Analysieren/Deskriptive Statistiken/Deskriptive Statistiken (Eine zweite Variante dazu ist unter Intervallschätzungen aufgezeigt.):
Abb. 2: Menüfolge zur Berechnung der Parameter der Stichprobe
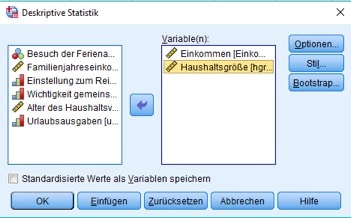
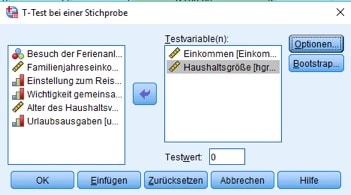
In der nächsten Dialogbox wählst Du die Dich gerade interessierenden Variablen aus.
Abb. 3: Dialogbox zur Auswahl der Variablen
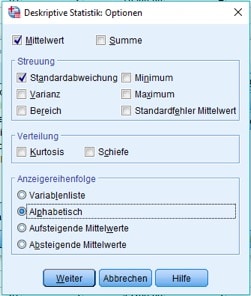
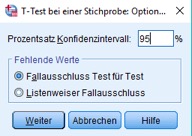
Klickst Du auf die Schaltfläche Optionen, so kannst Du genau angeben, welche Parameter Du gerade berechnen lassen möchtest:
Abb. 4: Dialogbox zur Optionswahl
Hier sind nur Mittelwert und Standardabweichung ausgewählt und die Ausgabe der Ergebnisse soll dabei alphabetisch erfolgen.
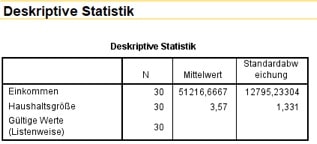
Sobald Du dann auf Weiter und OK geklickt hast, erhältst Du direkt Deinen Output, die Schätzwerte für die Grundgesamtheit.
Abb. 5: Output der berechneten Parameter
Für die inferenzielle Statistik ist der Schätzwert für den Mittelwert der Grundgesamtheit gerade der Mittelwert der Stichprobe. Bei der Standardabweichung berücksichtigt SPSS, dass bei kleinen Stichproben der Korrekturfaktor
zu verwenden ist. Vgl. dazu auch (Eckstein, 2016) oder beispielsweise die Erläuterungen der Uni Magdeburg.
Inferenzielle Statistik: Intervallschätzungen
Je größer der Umfang Deiner Stichproben ist, umso besser sind die Schätzwerte, die Dir die inferenzielle Statistik liefert. Trotzdem stimmen die zufallsüberlagerten Schätzwerte nur sehr selten exakt mit den wahren Werten überein.
Die inferenzielle Statistik kann Dir aber, ausgehend von diesen Schätzungen, Intervalle angeben, innerhalb deren Grenzen die wahren Werte mit einer von Dir gewählten Wahrscheinlichkeit liegen. Diese Bereiche heißen Konfidenzintervalle (Vgl. dazu auch Janssen/Laatz, 2017).
SPSS berechnet Dir die Konfidenzintervalle für die beiden Mittelwerte von Jahreseinkommen und Haushaltsgröße beispielsweise über die Menüfolge Analysieren/Mittelwerte/T-Test bei einer Stichprobe:
Abb. 6: Menüfolge zur Berechnung von Konfidenzintervallen
Du wählst wieder die Dich interessierenden Variablen aus.
Abb. 7: Dialogbox zur Auswahl der Variablen
Dann klickst Du auf Optionen, um den Prozentsatz festzulegen, mit welcher Wahrscheinlichkeit das Intervall den wahren Wert enthalten soll. Je größer Du diese Wahrscheinlichkeit wählst, umso sicherer ist zwar Deine Aussage, aber umso breiter und damit weniger aussagekräftig ist das Intervall. Die inferenzielle Statistik verwendet häufig eine Wahrscheinlichkeit von 95%.
Abb. 8: Auswahl des Prozentsatzes
Klickst Du auf weiter und dann auf OK, so erhältst Du zum einen die Punktschätzungen für Mittelwert und Standardabweichung auf die zweite mögliche Art und Weise. Im unteren Teil des Outputs findest Du dagegen die gesuchten Grenzen der beiden Konfidenzintervalle.
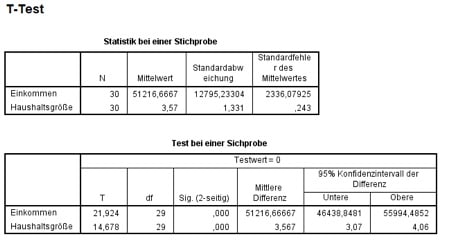
Abb. 9: Punkt- und Intervallschätzungen für Einkommen und Haushaltsgröße
Mit einer Wahrscheinlichkeit von 95% also liegt das durchschnittliche Einkommen in der Stadt zwischen 46.438,85 € und 55.994,49 €. Die mittlere Haushaltsgröße liegt ebenfalls mit 95% zwischen 3,07 und 4,06 Personen.
Die Breite des Konfidenzintervalls kannst Du reduzieren und damit die Genauigkeit der Schätzung erhöhen, indem Du entweder die Wahrscheinlichkeit kleiner oder den Stichprobenumfang größer wählst. Alternativ bietet sich Dir natürlich der Datenanalyse Service.
Testtheorie
Als dritten Bereich umfasst die inferenzielle Statistik die Testtheorie.
Du stellst hier Hypothesen über die Parameter der Grundgesamtheit auf und nimmst statistische Tests Deiner Stichprobe vor. Im obigen Beispiel könntest Du exemplarisch die Hypothese testen, dass das mittlere Jahreseinkommen in dieser Stadt unter 45.000 € liegt. Vor dem Test legst Du die Irrtumswahrscheinlichkeit, meist mit α=0,05, fest.
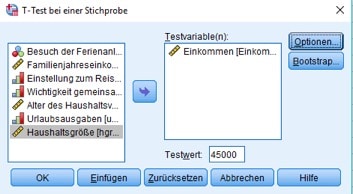
Dazu wählst Du in der SPSS Syntax wieder die Menüfolge der Abb. 6, nämlich Analysieren/Mittelwerte/T-Test bei einer Stichprobe. In der Dialogbox gibst Du als Testvariable das Einkommen ein und trägst den zu prüfenden Wert 45.000 unten als Testwert ein.
Abb. 10: Dialogbox für den Hypothesentest
Klicken auf OK liefert Dir Deinen Analyseoutput.
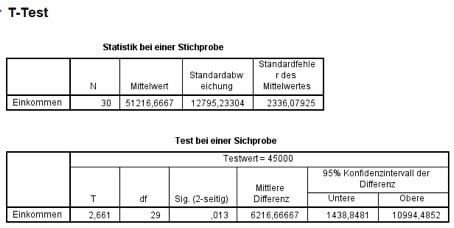
Abb. 11: SPSS-Output für den t-Test
Die Prüfgröße, der T-Wert, wäre im Vergleich mit der theoretischen t-Verteilung mit (n-1)=29 Freiheitsgraden im zweiseitigen Test also bei einer Irrtumswahrscheinlichkeit von 0,013 signifikant. Da Du hier ja einseitig testest, ob nämlich das Jahreseinkommen kleiner ist als 45.000 €, verdoppelst Du diesen Wert zu p=0,026.
Deine Nullhypothese ist dabei zu verwerfen, wenn p<α. Das ist hier mit 0,026<0,05 natürlich der Fall und Du schließt also, dass das mittlere Jahreseinkommen nicht unter 45.000 € liegt.
Die inferenzielle Statistik mit SPSS erlaubt Dir also zum einen, anhand der Stichprobe Punkt- oder Intervallschätzungen etwa für den Mittelwert der Grundgesamtheit zu treffen, zum anderen, Hypothesen über die unbekannte Grundgesamtheit zu treffen. Bei Unsicherheiten ist der Statistik-Service ratsam.
Falls Du eine sehr kleine Stichprobe hast und keine Normalverteilung für die Grundgesamtheit annehmen kannst, solltest Du in SPSS die nichtparametrischen Verfahren über die Menüfolge Analysieren/Nichtparametrische Test verwenden.
Literatur
Eckstein, Peter P (2016): Angewandte Statistik mit SPSS, 8. Auflage, Berlin.
Janssen, Jürgen/Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage, Berlin.
Springer Fachmedien Wiesbaden (Hrsg.)(2013): Kompakt-Lexikon Wirtschaftsmathematik und Statistik, Wiesbaden.