Was ist univariate Statistik mit SPSS?
Die univariate Statistik im Allgemeinen analysiert einzelne Variablen, ohne sich um eventuell vorhandene Einflussgrößen oder Zusammenhänge zu kümmern. Insofern handelt es sich um simple Analysen, die Du ganz einfach mit SPSS durchführen kannst. Oft schließt sich dann an die univariate Statistik die bivariate Statistik in SPSS und daran anknüpfend eine bivariate oder multivariate Analyse an. Damit kannst Du dann Beziehungen zwischen den Variablen herausarbeiten (vgl. Benninghaus, 2013).
In jedem Fall aber ist das Skalenniveau in SPSS der jeweils erhobenen Daten für Deine univariate Statistik wichtig. Es ist vor allem dafür verantwortlich, was für Aussagen Du anhand der Daten treffen kannst. Wenn Du Dir nicht sicher ist, welche Aussagen aus Deinen Daten hervorgehen, dann ist der Statistik-Service ratsam.
Übersicht über die Skalenniveaus
In der Statistik kannst Du zunächst drei verschiedene Skalenniveaus unterscheiden (vgl. Fahrmeir et al., 2016):
- Nominalskala: Hier gibt es zwar unterschiedliche Ausprägungen eines Merkmals, die sich für die Dateneingabe numerisch codieren lassen. Du kannst sie aber nicht in eine Rangfolge bringen, geschweige denn Unterschiede messen.
- Ordinalskala: Dazu gehören Merkmale, deren jeweilige Ausprägungen sich in eine Rangfolge bringen lassen, ohne dass Du aber die Abstände zwischen den Ausprägungen messen kannst.
- Metrische Skala: Liegen Dir dagegen numerische Werte vor und kannst Du mit diesen Werten rechnen, dann hast Du metrische Merkmale gegeben. Du kannst damit also Differenzen oder Quotienten ermitteln.
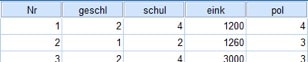
Stell Dir vor, Du hast gerade die Besucher einer Veranstaltung befragt. Erhoben hast Du dabei ihr Geschlecht, ihren höchsten Schulabschluss, weiter ihr Nettoeinkommen und ihren Grad des Interesses an Politik:
Abb. 1: Dein SPSS-Datensatz
Dann liegt Dir mit Geschlecht dementsprechend ein nominalskaliertes Merkmal vor. Es lässt sich nur die Zuordnung zu einer der beiden möglichen Kategorien feststellen, aber Du kannst keine Rangordnung dazwischen ausmachen.
Mit dem „höchsten Schulabschluss“ und auch mit dem „Grad des politischen Interesses“ hast Du dagegen zwei ordinalskalierte Merkmale gegeben: Du weißt zwar, dass sehr großes politisches Interesse mehr ist als wenig Interesse, der Abstand kann aber nicht in Zahlen angegeben werden.
Das monatliche Nettoeinkommen hingegen ist metrisch skaliert. Wer 1500 € im Monat zur Verfügung hat, kann genau doppelt so viel ausgeben wie jemand, der 750 € bezieht.
Deskriptive (beschreibende) univariate Statistik mit SPSS
Wenn Dich gerade die Kennzahlen der Datenverteilung in SPSS Deiner Stichprobe interessieren, so berechnest Du durch deskriptive Statistik eindeutige Werte.
Die in den Daten enthaltenen Informationen nehmen also von der Nominalskala über die Ordinalskala zur metrischen Skala hin zu. Entsprechend kannst Du natürlich auch umso differenziertere Aussagen treffen, je höher das Skalenniveau liegt. Entsprechend wählst Du danach die passenden Verfahren für die univariate Statistik aus.
Vgl. dazu auch die Hinweise des Gabler Wirtschaftslexikons.
Häufigkeiten
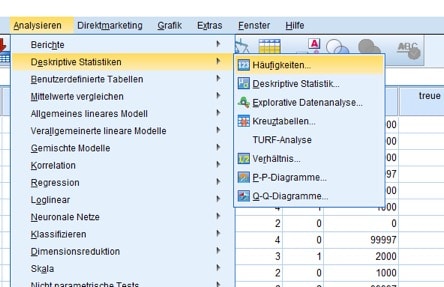
Zunächst möchtest Du für die univariate Statistik eine Auszählung der Häufigkeiten erhalten. Dazu wählst Du in der SPSS Syntax den Befehl Analysieren/Deskriptive Statistiken/Häufigkeiten.
Abb. 2: Menüfolge zur Bestimmung der Häufigkeiten
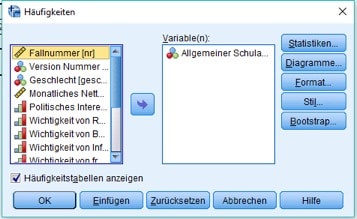
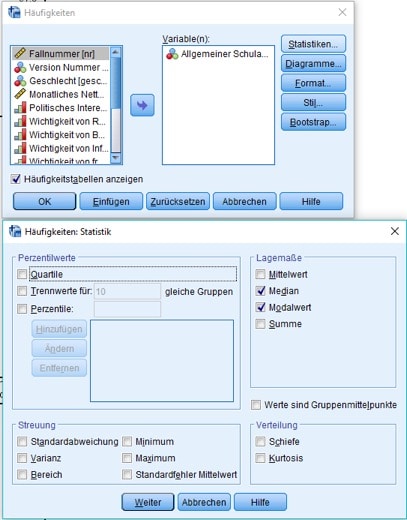
Im nachfolgenden Fenster wählst Du dann auf der linken Seite die gerade gewünschte Variable. Du klickst danach auf den Button mit dem Pfeil und sie wird dadurch in der Mitte des Fensters hinzugefügt.
Abb. 3: SPSS-Dialogbox zur Auswahl der Variablen
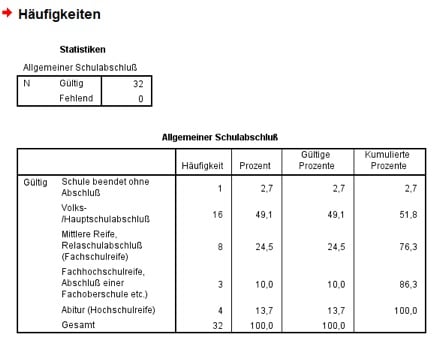
Danach klickst Du wieder auf OK und erhältst sofort die ausgezählten Häufigkeiten:
Abb. 4: SPSS-Output der Häufigkeiten
Lagemaße
Wichtige Kennzahlen für die univariate Statistik sind Lageparameter. Hierzu zählen Mittelwert, Median und Modus. Sie beschreiben, um welchen zentralen Wert herum die Beobachtungen liegen:
- Modus oder Modalwert ist der Wert, der am häufigsten auftritt. Du kannst ihn für jedes Skalenniveau, also auch schon für nominalskalierte Werte, bestimmen.
- Median oder Zentralwert ist der Wert, unter und über dem jeweils genau 50 % der Beobachtungen liegen. Ordnest Du alle Beobachtungen der Größe nach an, liegt er also genau in der Mitte. Der Median erfordert mindestens ein ordinales Skalenniveau.
- Mittelwert ist der durchschnittliche Beobachtungswert und kann folglich nur bei metrisch skalierten Werten ausgerechnet werden.
Die Lageparameter für die univariate Statistik kannst Du mit der SPSS Software ganz einfach ermitteln. Du solltest aber in jedem Fall wieder vor der Berechnung überlegen, welche Lageparameter für das Skalenniveau Deiner Merkmale jeweils passen. Solltest Du Dir hier unsicher sein, so empfiehlt sich die Statistik Nachhilfe.
Wie oben startest Du die Menüfolge Analysieren/Deskriptive Statistiken/Häufigkeiten (siehe Abb. 1). Dort wählst Du die Dich gerade interessierenden Variablen in der Dialogbox aus und klickst auf „Statistiken“:
Abb. 5: Auswahl der Lageparameter in SPSS
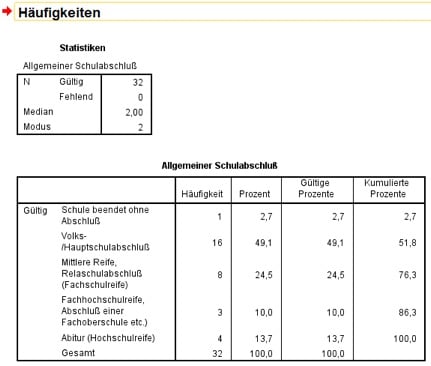
Hier wurden entsprechend für das Merkmal „höchster Schulabschluss“ nur die beiden Lageparameter Median und Modalwert für die univariate Statistik ausgewählt. Die Berechnung des Mittelwerts ist ja wegen des ordinalen Skalenniveaus nicht sinnvoll.
Durch Klicken auf „Weiter“ und „OK“ erhältst Du direkt die Ergebnisse:
Abb. 6: Ausgabe der Lageparameter
Im oberen Part der Ausgabe siehst Du dabei, dass sowohl der Median, also der mittlere beobachtete Wert, als auch der Modus, das ist ja der häufigste beobachtete Wert, beide bei 2 liegen. Schaust Du Dir darunter die Häufigkeiten an, so erkennst Du, wie diese beiden Werte zustande kommen.
Streuungsmaße
Zusätzlich zu den Lageparametern kann Dir die univariate Statistik auf gleiche Art Streuungsparameter in SPSS berechnen, von denen wohl die bekanntesten und meist verwendetsten sind:
- Varianz, die die durchschnittliche quadratische Abweichung der Beobachtungswerte von ihrem Mittelwert angibt (erfordert metrische Daten), sowie
- Standardabweichung, die die Wurzel aus der Varianz ist (erfordert genauso metrische Daten).
- Spannweite hingegen ist die Differenz zwischen dem größten und kleinsten beobachteten Wert.
Induktive (schließende) univariate Statistik in SPSS
Oft interessiert Dich dagegen nicht so sehr die univariate Statistik der Stichprobe, sondern Du möchtest eigentlich Aussagen über die unbekannte Grundgesamtheit treffen. Dann musst Du dafür auf die Überlegungen der Wahrscheinlichkeitstheorie oder den Datenanalyse Service zurückgreifen.
Du betrachtest dafür Dein Merkmal als Zufallsvariable X, das einer unbekannten Verteilung folgt, und die erhobenen Daten als Realisationen dieser Zufallsvariablen. Eine gute Zusammenstellung findest Du beispielsweise auf der Internet-Seite der Mathematical Image Analysis Group der Universität des Saarlands.
Dann liefert Dir die univariate Statistik Schätzwerte für die unbekannten Parameter, Erwartungswert und Standardabweichung. Anschließend kannst Du beispielsweise einen t-Test durchführen. Das statistische Verfahren eignet sich, um in Erfahrung zu bringen, ob der Mittelwert der Grundgesamtheit kleiner als ein von Dir vorgegebener Wert ist.
Die univariate Statistik wird als erstes Instrumentarium der Analyse auf fast jede Datenverteilung in SPSS angewendet. Sie liefert Dir nämlich einen schnellen Überblick über die Kerninformationen Deiner Daten. Daran kannst Du dann entscheiden, welche Verfahren gegebenenfalls weiterverwendet werden sollen.
Literatur
Benninghaus, Hans (2013): Deskriptive Statistik: Eine Einführung für Sozialwissenschaftler, 9. Auflage, Heidelberg.
Fahrmeir, Ludwig/Heumann, Christian/Künstler, Rita (2016): Der Weg zur Datenanalyse, Heidelberg.