Normalverteilung mit SPSS

Eine Normalverteilung mit SPSS überprüfen: Viele statistische Tests benötigen die Normalverteilung als Voraussetzung. Damit Du solche Verfahren verwenden kannst, musst Du daher zunächst prüfen, ob eine Annahme der Normalverteilung mit Deinen Daten vereinbar ist.

Der Shapiro-Wilk-Test ist ein Test auf Normalverteilung für metrische Daten, den Du schon bei sehr kleinen Stichprobenumfängen, genauer gesagt, ab n=3, einsetzen kannst. Trotz der geringen Voraussetzungen an den Stichprobenumfang besitzt er dennoch eine verhältnismäßig hohe Trennschärfe (vgl. Janssen/Laatz 2017).

Wenn das Testergebnis nicht gegen die Normalverteilungsannahme spricht, können folglich parametrische Verfahren, die Normalverteilung voraussetzen, auch auf diese kleine Stichprobe angewendet werden. Natürlich müssen die anderen Voraussetzungen ebenfalls erfüllt sein. Wenn Du mit den Voraussetzungen nicht vertraut bist, empfiehlt sich die Statistik Nachhilfe.

Du kannst den Shapiro-Wilk-Test schnell und unkompliziert mit der SPSS Software durchführen.

Normalverteilung mit SPSS: Datensatz und Nullhypothese für den Shapiro-Wilk-Test

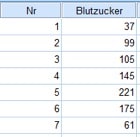
Im Rahmen einer medizinischen Untersuchung hast Du an sieben Testpersonen unter anderem den Blutzuckerwert erhoben.

Abb. 1: Blutzuckerwerte der Probanden

Für jede weitere von Dir geplante statistische Analyse müsste die Voraussetzung gegeben sein, dass die Blutzuckerwerte einer Normalverteilung folgen. Um dies zu belegen, entschließt Du Dich, den Shapiro-Wilk-Test auf das Datenmaterial anzuwenden.

Dieser prüft die Nullhypothese zu einer Irrtumswahrscheinlichkeit α. Verwirfst Du die Nullhypothese nicht, so gibt es aufgrund des Tests keinen Anlass, die geplanten Verfahren nicht anzuwenden.

Konstruktion der Teststatistik und Testentscheidung

Als Teststatistik dafür dient der Quotient zweier Schätzungen für die Varianz:

• einer testspezifisch berechneten Varianz, die unter der Annahme der Normalverteilung zu erwarten wäre, und
• der Stichprobenvarianz.

Falls die Normalverteilung gilt, sollten beide Schätzwerte ähnlich ausfallen und der Quotient sollte in der Nähe von Eins liegen.

Du verwirfst dann die Nullhypothese, wenn die Prüfgröße kleiner als ein testspezifischer kritischer Wert ist. Dieser ist von der Form der Schätzfunktion und damit vom Stichprobenumfang abhängig sowie von der Irrtumswahrscheinlichkeit α (Vgl. dazu auch Holling/Gediga 2016). Bei Unsicherheiten bietet sich der Statistik-Service an.

SPSS umfasst den Shapiro-Wilk-Test und hat in der SPSS Syntax sowohl die testspezifischen kritischen Werte als auch die Berechnungsmodalitäten für die Varianz des Zählers Deiner Teststatistik implementiert. Du kannst daher die Testentscheidung sehr einfach treffen, indem Du die berechnete Signifikanz p mit Deiner Irrtumswahrscheinlichkeit vergleichst.

Durchführung des Shapiro-Wilk-Test auf Normalverteilung mit SPSS

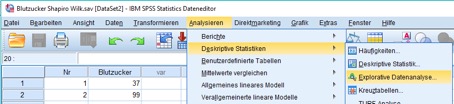
Für die Durchführung des Tests mit SPSS wählst Du daher die Menüfolge Analysieren/Deskriptive Statistiken/Explorative Datenanalyse.

Abb. 2: Menüfolge für den Shapiro-Wilk-Test

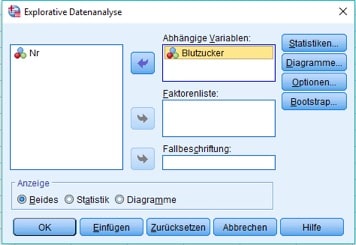
Daraufhin öffnet sich die Dialogbox „Explorative Datenanalyse“, in der Du die zu untersuchende Variable durch Anklicken und Klicken auf den Pfeil nach rechts auswählst, in diesem Fall ist es der Blutzucker.

Abb. 3: Dialogbox „Explorative Datenanalyse“

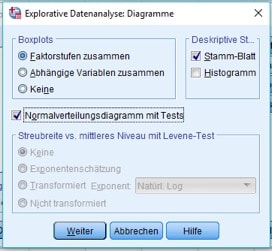
Klicke auf den Button „Diagramme“ und Du erhältst wieder eine weitere SPSS-Dialogbox.

Abb. 4: Dialogbox „Explorative Datenanalyse: Diagramme“

Hier setzt Du bei „Normalverteilungsdiagramm mit Tests“ einen Haken und startest den Test durch Klicken auf „Weiter“ und dann auf „OK“.

Die Testentscheidung über Normalverteilung anhand des SPSS-Outputs

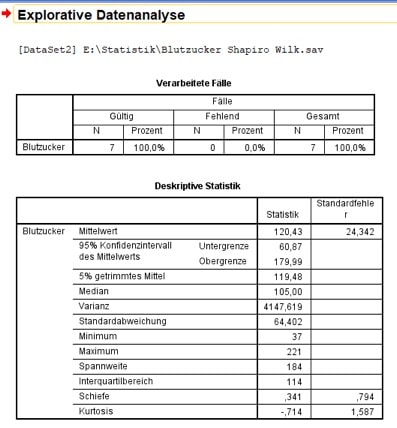
Anschließend erhältst Du einen mehrteiligen Output. Ganz oben siehst Du zuerst, wie viele gültige, fehlende und wie viele Fälle insgesamt vorliegen. Daran schließt sich zum Teil die deskriptive Statistik an, die allerdings für unser Thema nicht wichtig ist.

Abb. 5: Oberer Teil Deines SPSS-Outputs

Im folgenden Teil des Outputs liefert Dir SPSS die Resultate der beiden häufigen Tests zu unserem Thema: Kolmogorov-Smirnov- sowie Shapiro-Wilk-Test.

Abb. 6: Unterer Teil des SPSS-Outputs mit Shapiro-Wilk-Test

Die Teststatistik, die wie oben angegeben der Quotient zweier Varianzen ist, liegt demnach mit 0,974 in der Nähe von Eins. Das kann Dir bereits als Anzeichen dafür dienen, dass eine Normalverteilung vorliegen könnte. Die Testentscheidung triffst Du anschließend im Vergleich zwischen der im Vorhinein festgelegten Irrtumswahrscheinlichkeit α, die hier als α=5% gewählt ist, und der für die Testgröße berechneten Signifikanz p.

Ist α größer als die berechnete Signifikanz, so verwirfst Du Deine Nullhypothese. Anderenfalls gibt dir die Datenverteilung in SPSS keinen Anlass dazu. Hier liegt die berechnete Signifikanz mit 0,926 deutlich über 0,05. Damit liefert das Datenmaterial keinen Grund dafür, die Nullhypothese zu verwerfen.

Für Dein weiteres Vorgehen heißt das: statistische Verfahren, die die Annahme der Normalverteilung erfordern, dürfen auf Dein Datenmaterial angewendet werden.

Bewertung des Tests auf Normalverteilung

Zum gleichen Resultat kommst Du hier auch mit dem Kolmogorov-Smirnov-Test, wenn Du dessen berechnete Signifikanz aus der Abbildung 6 mit der gewählten Irrtumswahrscheinlichkeit vergleichst.

Der Shapiro-Wilk-Test erlaubt ausschließlich die Überprüfung, ob Deine Daten mit der Annahme der Normalverteilung vereinbar sind. Er kann nicht für andere Verteilungen verwendet werden, trennt dafür aber schon bei sehr kleinen Stichprobengrößen recht scharf. Er kann ab einem Stichprobenumfang von n=3 angewendet werden.

Für die Prüfung ist daher der Shapiro-Wilk-Test immer vorzuziehen. Vergleiche dazu auch die Ausführungen der Universität Würzburg.

Möchtest Du dagegen prüfen, ob Deine Daten zu der Annahme einer anderen Verteilung als der Normalverteilung passen, solltest Du den Kolmogorov-Smirnov-Test anwenden. Er ist vielseitiger, aber nicht so trennscharf wie der Shapiro-Wilk-Test. Alternativ bietet sich Dir die Option des Datenanalyse Service.

Setzt ein statistisches Verfahren die Annahme der Normalverteilung voraus, so solltest Du Deine Daten mit Hilfe des Shapiro-Wilk-Test darauf untersuchen, ob sie dieser Annahme standhalten. Die Durchführung dieses Tests ist mit SPSS sehr unkompliziert und schnell zu bewerkstelligen.

Literatur

Holling, Heinz/Gediga, Günther (2016): Statistik-Testverfahren, 1. Auflage, Göttingen.

Janssen, Jürgen/Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage, Berlin.