Regressionsanalyse in SPSS

Durch Regressionsanalyse mit SPSS kannst du Trends erkennen und voraussagen. Du kannst ebenso Ursache und Wirkung begründen und Zusammenhänge zwischen Variablen erkunden. Eine typische Fragestellung ist hier beispielsweise: „Hat eine Variable Einfluss auf eine andere?“ oder „Wie stark ist der Zusammenhang zwischen den Variablen?“.

Ziele der Regressionsanalyse mit SPSS

Mithilfe der Regressionsanalyse mit SPSS kannst du außerdem gewisse statistische, unternehmerische und wissenschaftliche Ziele verfolgen. Du kannst zudem die Regressionsanalyse mit SPSS ebenso zur Trendbestimmung einsetzen, aber auch Ursachen und deren Wirkung aufspüren. Schließlich kannst Du sogar Zusammenhänge und deren Stärke erklären (vgl. Wooldridge, 2013).

Beispiele:

• Gibt es einen Zusammenhang zwischen Intelligenz und Lernerfolg?
• Hat das Einkommen einen Einfluss auf die Gesundheit der Mitarbeiter?
• Welche Auswirkung hat eine Marketingstrategie auf die Verkaufszahlen eines Produktes?

In diesem Leitfaden wird die bivariate und multivariate lineare Regression mit der SPSS Software erläutert. Du kannst die bivariate Regression in SPSS umsetzen, in Anlehnung an die Bivariate Statistik in SPSS. Dabei ist es beispielsweise möglich, eine beobachtete Variable durch eine andere Variable zu erklären. Die multivariate lineare Regression lässt sich aber ebenso in SPSS nutzen. Hiermit kannst Du beispielsweise, im Rahmen der Korrelation in SPSS, den Zusammenhang zwischen einer beobachteten Variable und mehrere anderer Variablen bestimmen. Dabei sind die abhängige(n) und unabhängige(n) Variable(n) linear miteinander verknüpft. Bevor Du die Ergebnisse der Regression jedoch bewertest, prüfe, ob gewisse Voraussetzungen für die Gültigkeit der linearen Regression erfüllt sind. Bei Fragen kannst du dich an den Statistik Service wenden.

Allgemein gilt die Formel

Voraussetzung der lineare Regression mit SPSS

Damit Du eine gültige Aussage mit der Regressionsanalyse treffen kannst, solltest Du gewisse Voraussetzungen der linearen Regression prüfen. Einige Hinweise für deren Untersuchung in SPSS kannst Du im Folgenden nachlesen.

Metrische Messung

Die abhängige Variable soll metrisch gemessen vorliegen. Das ist dann der Fall, wenn Du die Beobachtung auf einer metrischen Messskala durchgeführt hast. Unterformen sind hier die Intervallskala, Verhältnisskala und Absolutskala. Beispiele hierfür sind das Alter der Versuchspersonen, das Körpergewicht, Längenmaße, die Stückzahl des verkauften Produktes, die Temperatur in Grad Celsius, Kalenderzeiten.

Zufallsstichprobe

Weiterhin sollte als Voraussetzung der linearen Regression gelten: Die Messung stammt aus einer zufälligen Stichprobe und weist daher keine systematischen, durch die Gewinnung der Stichprobe bedingten, Fehler auf.

Bedingter Erwartungswert

Der Erwartungswert soll zusätzlich im Durchschnitt den Wert 0 annehmen. Erstelle zur Überprüfung eine grafische Darstellung in SPSS.  So erzeugst du ein Punktdiagramm der standardisierten, geschätzten Werte von Y und der standardisierten Fehlerwerte. Die Voraussetzung ist dann gültig, wenn in etwa gleich viele Werte über und unterhalb der Nulllinie im Diagramm liegen. Bei Problemen kannst du dich an einen Datenanalyse Service wenden.

Homoskedastizität mit SPSS

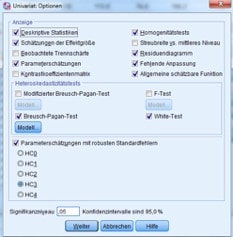
In einem Diagramm kannst Du ebenfalls eine weitere Voraussetzung der linearen Regression prüfen. Nämlich, ob jeder Wert der unabhängigen Variablen des Fehlerwertes dieselbe Varianz hat (Voraussetzung der Homoskedastizität). Erkennst Du im Diagramm ein Muster, das einer Posaune oder einem Trichter ähnelt, ist diese Annahme dementsprechend verletzt. Weitere statistische Tests können in SPSS dann mittels Breusch-Pagan-Test (vgl. Wooldridge, 2013) oder White-Test vorgenommen werden. Dies ist ab der SPSS Version 25 unter der Auswahl Analysieren > allgemeines lineares Modell > Univariat… möglich. Die Nullhypothese kannst Du dann nicht verwerfen, wenn ein Signifikanz-Wert größer als 0,05 ermittelt wird. Ist das Testergebnis signifikant, liegt also die Vermutung der Heteroskedasdizität nahe. Wenn die Voraussetzung verletzt ist, kannst Du die Variable transformieren. Ab der SPSS Version 25 hast Du außerdem die Wahl, die Schätzung der Parameter mit robusten Standardfehlern durchzuführen. Voreingestellt ist hier die Variante HC3. Diese wird bei Stichproben kleiner oder gleich n= 250 empfohlen.

Abbildung 1: Allgemeines lineares Modell zur Auswahl von Schätzverfahren mit robusten Standardfehlern

Lineare Regression mit SPSS

Die abhängige(n) und unabhängige(n) Variable(n) sollen zudem in einem linearen Zusammenhang stehen. Obgleich ein linearer Zusammenhang vorliegt, prüfst du in SPSS wiederum mit Diagrammen. Erstelle zuerst ein einfaches Punktdiagramm der abhängigen und jeder einzelnen unabhängigen Variable. Prüfe dann, ob Du einen linearen Zusammenhang im Diagramm erkennen kannst. Ist dies der Fall, kannst du die Annahme der Linearität bestätigen. Falls kein linearer Zusammenhang vermutet wird, kannst Du durch geschickte Transformation die Daten in Richtung eines linearen Zusammenhanges bringen, beispielsweise durch logarithmieren der Variablen.

Normalverteilung der Fehlerwerte dank SPSS finden

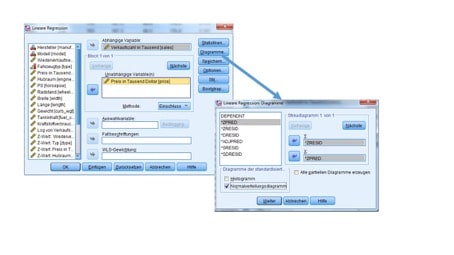
Ob die Fehlerwerte Deiner linearen Regression annähernd einer Normalverteilung in SPSS unterliegen, kannst Du wieder mit einem Sichtungstest prüfen. Fertige dazu in SPSS ein P-P Diagramm an (Vgl. Abbildung 2).

Abbildung 2: Anfertigen eines Diagramms zur Überprüfung auf Normalverteilung der Fehler

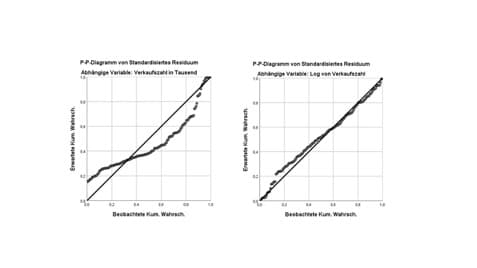
In der Abbildung 3 liegt links keine Normalverteilung der Fehler vor. Dies erkennst Du an der geschlungenen Punkte-Linie um die Diagonale. Hiermit ist eine Voraussetzung zur gültigen Annahme der linearen Regression verletzt. Abhilfe kann eine Transformation der abhängigen Variable schaffen. Du kannst dazu dank der SPSS Syntax beispielsweise den Logarithmus anwenden. Nachdem Du die zu erklärende Variable umgerechnet hast, erkennst Du im P-P-Diagramm (rechts in der Abbildung) eine annähend normalverteilte Datenlage der Fehler. Im P-P-Diagramm befinden sich die Punkte nahe an oder direkt auf der diagonalen Line. Nun ist die Voraussetzung gegeben und Du kannst die Regressionsanalyse fortsetzen.

Abbildung 3: P-P-Diagramm zur Prüfung auf Normalverteilung der Fehler in der linearen Regression

Unabhängigkeit des Fehlerwertes mit SPSS

Vergewissere dich in der Regressionsanalyse immer, dass die Fehlerterme der Beobachtungen nicht zusammenhängen. Unabhängige Fehlerwerte kannst du in der Regressionsanalyse in SPSS mit dem sogenannten Durbin-Watson-Test überprüfen. Der Kennwert des Tests kann die Ausprägungen zwischen 0 und 4 annehmen. Ist der Wert in etwa 2, kannst Du die Fehler als unabhängig annehmen.

Keine Multiliniarität

Eine weitere Voraussetzung der Regressionsanalyse ist, dass die unabhängigen Variablen im Falle einer multivariaten linearen Regression in SPSS tatsächlich unabhängig sind. Siehe mithilfe von SPSS auf den Toleranzwert und den Varianzinflationsfaktor „VIF“. Per Daumenregel soll der Toleranzwert nicht unterhalb von 0,10 liegen. Der Wert des sogenannten „VIFs“ darf nicht oberhalb von 10 sein.

Eine weitere Hilfe zu den Voraussetzungen der linearen Regression findest Du auf dem Blog eines Professors der University of Sussex.

Beispielfall für eine Regressionsanalyse mit SPSS

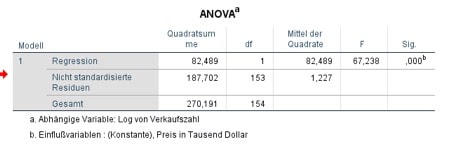
Im vorliegenden Beispiel regressiert die Variable „Verkaufszahlen“ den „Preis des Autos“. Mittels F-Test kannst Du das Modell bewerten. Betrachte dazu zuerst die ANOVA Tabelle. Hier kannst Du entnehmen, ob das Modell insgesamt signifikant ist. Wird die Vorhersage der abhängigen Variable „Log Verkausfszahl“ durch das Hinzunehmen der unabhängigen Variable „Preis des Autos in Tausend“ verbessert? Betrachte nun die Ausgabe von SPSS, dann erkennst Du, dass das Ergebnis F(153)= 67,24 mit einem p-Wert <0,001 signifikant ist (vgl. Abbildung 4). Somit kannst Du die Regressionsanalyse fortsetzen.

Abbildung 4: Anova Tabelle in SPSS innerhalb der linearen Regression

Abbildung 5: Modellzusammenfassung in SPSS

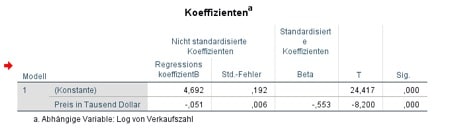
Das Modell klärt knapp 30% der Varianz auf (vgl. Abbildung 5). Nun kannst du die Koeffizienten (vgl. Abbildung 6) der linearen Regression bewerten. Der jeweilige t-Test zeigt Dir, ob der Achsenabschnitt und die Konstante der Messvariable gültig ist. Hier ist sowohl der t-Test der Konstanten und des Koeffizienten „Preise in Tausend Dollar“ signifikant. Das Ergebnis der Regressionsanalyse kannst Du somit folgendermaßen bewerten.

Abbildung 6: Koeffizienten der Regressionsanalyse mit SPSS

Erhöht sich der Preis in Tausend um eine Einheit, so verringert sich die Verkaufszahl annäherungsweise um 5%. Beachte hier, dass die abhängige Variable logarithmiert vorliegt. Ist dies nicht der Fall, interpretierst du die Koeffizienten je nach Vorzeichen und Steigung. Ein Koeffizient von = 0,05 würde beispielsweise bedeuten, dass eine Erhöhung um eine Einheit, Y im Durchschnitt um 0,05 Einheiten erhöht.

Letztendlich empfiehlt es sich, mittels SPSS die Voraussetzungen der Regressionsanalyse zu prüfen (vgl. Field 2017). Dazu kannst Du auf Kennzahlen oder auf Grafiken zurückgreifen. Sind die Voraussetzungen der linearen Regression erfüllt, kannst Du Dein Modell anwenden und Prognosen, Zusammenhänge oder Hypothesen testen. Hilfe bei Problemen und Fragen kann dir eine Statistik Beratung geben.

Literatur

Field, Andy (2017): Discovering Statistics Using IBM SPSS Statistics, 5. Auflage London.

Wooldridge, Jeffery (2013): Introductory Econometrics: A modern approach, 5. Auflage Mason (OH).