Ein Mediantest ist ein nicht parametrisches Verfahren, das zwei Stichproben darauf überprüft, ob sie sich bezüglich ihrer zentralen Tendenz unterscheiden. Damit stellt er eine Alternative zum sehr bekannten t-Test für den Mittelwertvergleich dar, wenn dessen enge Voraussetzungen nicht erfüllt sind. Der t-Test setzt schließlich metrisches Datenmaterial voraus, für das eine Normalverteilung angenommen werden kann.
Oft aber erlauben es die Daten nicht, von einer Normalverteilung der untersuchten Merkmale auszugehen und/oder Dein Datenmaterial ist nur ordinalskaliert. Dann liefern Dir die nicht parametrischen Verfahren alternative statistische Tests über die zentralen Tendenzen Deiner Stichproben. Statistische Verfahren wie diese arbeiten nämlich ohne Verteilungsannahmen und benötigen daher auch keine Schätzung von Parametern zu deren Beschreibung. Die bekanntesten und in SPSS implementierten Verfahren sind
- der Wilcoxon-Vorzeichen-Rang-Test, wenn Du verbundene Stichproben betrachtest, und
- der U-Test oder Mann-Whitney Test für den Vergleich zweier unabhängiger Stichproben.
Anschauliche Hilfe zu diesen verschiedenen Testverfahren findest Du beispielsweise bei diesem Überblick der Universität Frankfurt.
Mediantest mit SPSS für abhängige Stichproben
Man spricht von abhängigen Stichproben, wenn an einer Reihe von Merkmalsträgern ein Merkmal zu verschiedenen Zeitpunkten erhoben wurde. Ein Sportstudio beispielsweise erhebt an den Teilnehmern eines Muskelaufbauprogramms den Muskelanteil an der Körpermasse zu Beginn und am Ende dieses Projektes. Dann gehören je zwei Messungen zusammen, man spricht auch von gepaarten oder verbundenen Stichproben.
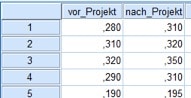
Dein Datensatz sieht dann etwa so aus:
Abb. 1: Muskelanteil bei Teilnehmern eines Muskelaufbauprogrammes vor und nach der Durchführung
Der für zwei abhängige Stichproben am häufigsten verwendete nicht parametrische Test ist der Wilcoxon-Vorzeichen-Rang-Test. Dieser prüft die Nullhypothese, die zentralen Tendenzen der Stichproben zu den beiden Zeitpunkten seien gleich. Dazu berechnet er jeweils die Differenzen beider Messungen und daraus dann zum einen die Absolutbeträge der Differenzen, die der Größe nach geordnet werden. Zum anderen ermittelt er die Vorzeichen der Differenzen. Wenn Dir der Wilcoxon-Vorzeichen-Rang-Test Schwierigkeiten bereitet, empfiehlt es sich, auf Statistik Nachhilfe zurückzugreifen.
Dann summiert er die Rangwerte aller Differenzen, zu denen ein positives Vorzeichen gehört sowie die derjenigen, zu denen ein negatives Vorzeichen zugeordnet ist. Das Minimum dieser beiden Summen ist die Prüfgröße, die dann mit einem testspezifischen kritischen Wert verglichen wird.
Ist die Prüfgröße größer als der kritische Wert, so verwirfst Du die Nullhypothese und schlussfolgerst, dass eine signifikante Änderung erfolgt ist.
Je nach Datenlage, das heißt nach Anzahl der verbundenen Stichproben sowie des Vorkommens von Bindungen usw. stehen in der SPSS Software weitere Tests zur Verfügung (vgl. Janssen/Laatz 2017).
Mediantest-Durchführung mit SPSS für abhängige Stichproben
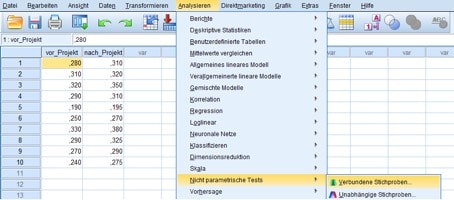
Um den Mediantest durchzuführen, wählst Du die Menüfolge Analysieren/Nicht parametrische Tests/Abhängige Stichproben.
Abb. 2: Menüfolge für den Mediantest bei abhängigen Stichproben
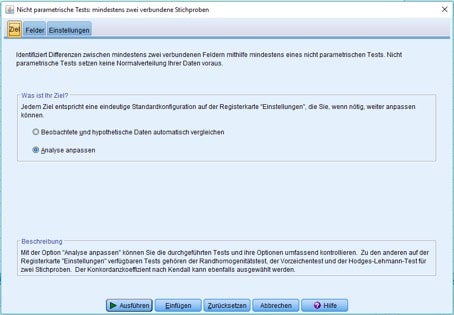
Es öffnet sich danach eine Dialogbox mit drei Registerkarten. Im ersten Register „Ziel“ wählst Du die Alternative „Analyse anpassen“.
Abb. 3: Register „Ziel“/unabhängige Stichproben
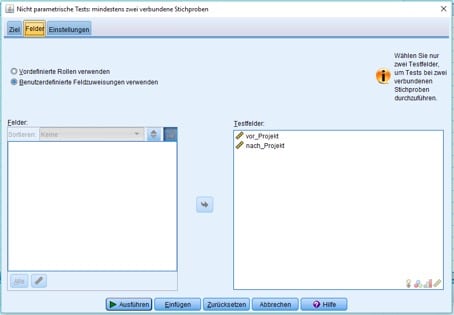
Im zweiten Register „Felder“ wählst Du diejenigen Variablen aus, die Du dem Mediantest unterziehen möchtest, also hier „vorProjekt“ und „nachProjekt“.
Abb. 4: Register „Felder“/abhängige Stichproben
Im dritten Register kannst Du dann den gewünschten Test und Testoptionen auswählen (vgl. auch Holling/Gediga 2016). In der Regel solltest Du aber, wie hier erfolgt, SPSS anhand der Daten den geeignetsten Test auswählen lassen.
Abb. 5: Register „Einstellungen“ / abhängige Stichproben
Klickst Du dann auf „Ausführen“, so erhältst Du direkt Deinen Output.
Abb. 6: Output vom Mediantest für verbundene Stichproben
SPSS hat hier, wie es gemäß der SPSS Syntax zu erwarten ist, den Wilcoxon-Vorzeichen-Rang-Test ausgewählt, da er für deine Daten am besten passt. Das berechnete Signifikanzniveau beträgt p=0,005. Legst Du die übliche Irrtumswahrscheinlichkeit von α=5% zugrunde, so lautet Deine Testentscheidung entsprechend: Mit 0,005=p<α=5% wird die Nullhypothese verworfen. Du schließt demnach auf signifikante Änderungen des Anteils der Muskelmasse bei den Probanden, die an dem Programm teilgenommen haben. Alternativ bietet sich natürlich der Datenanalyse Service an, mit dem du immer auf der sicheren Seite bist.
Mediantest für unabhängige Stichproben
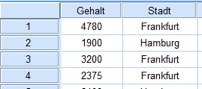
Lassen sich dagegen Beobachtungen der einen Stichprobe nicht denselben Merkmalsträgern einer anderen Stichprobe zuordnen, so spricht man von unabhängigen oder auch ungepaarten Stichproben. Stell Dir vor, Du möchtest beispielsweise die Anfangsgehälter von Hochschulabsolventen in den Städten Hamburg und Frankfurt miteinander vergleichen. Dich interessiert, ob es systematische Unterschiede in der Gehaltshöhe gibt. Daher erhebst Du in beiden Städten jeweils Stichproben im Umfang von acht Probanden.
Abb. 7: Gehälter von Hochschulabsolventen in Frankfurt und Hamburg
Es handelt sich also um kleine unabhängige Stichproben des metrischen Merkmals „Gehalt“. Wegen des geringen Stichprobenumfangs entschließt Du Dich, einen Mediantest durchzuführen. Ein häufig verwendeter Test bei zwei unabhängigen Stichproben wäre hingegen der U-Test auf Unterschiede in der zentralen Tendenz. Dessen Verallgemeinerung auf mehr als zwei Stichproben ist entsprechend der Kruskal-Wallis-Test oder H-Test.
Mediantest-Durchführung mit SPSS für unabhängige Stichproben
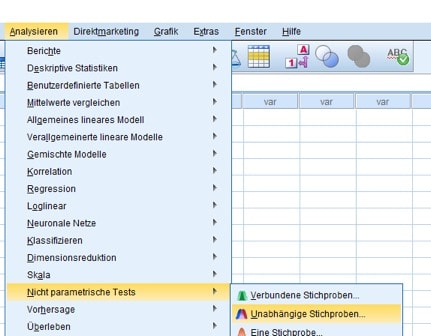
Um einen Mediantest für unabhängige Stichproben durchzuführen, wählst Du diesmal die Menüfolge Analysieren/Nicht parametrische Tests/Unabhängige Stichproben.
Abb. 8: Menüfolge für den Mediantest bei unabhängigen Stichproben
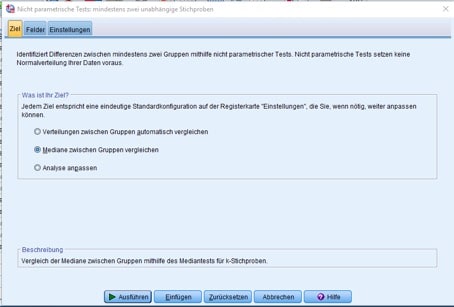
Es öffnet sich eine Dialogbox mit drei Registern. Im ersten Register „Ziel“ wählst Du die Option „Mediane zwischen Gruppen vergleichen.
Abb. 9: Register „Ziel“/unabhängige Stichproben
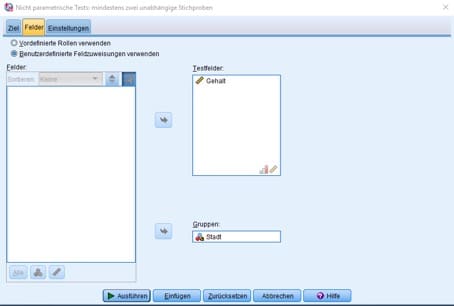
Im Register „Felder“ weist Du die Variablen in die passenden Bereiche ein: „Gehalt“ ist die zu testende Variable und „Stadt“ ordnet die Beobachtungen den jeweiligen Stichproben zu.
Abb. 10: Register „Felder“/unabhängige Stichproben
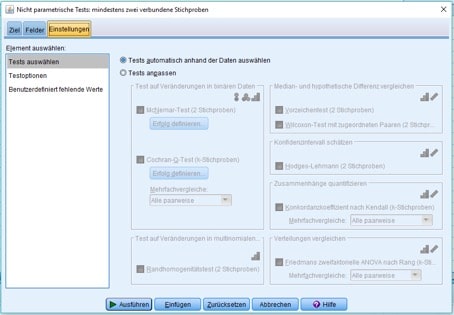
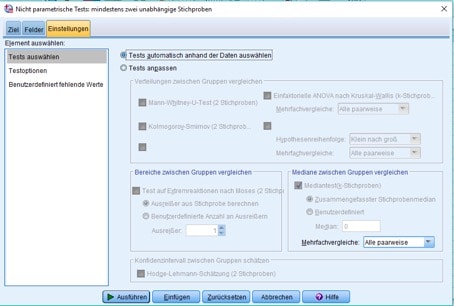
Im Register „Einstellungen“ wählst Du schließlich aus, welchen Test Du durchführen lassen möchtest. In der Regel bietet es sich an, SPSS den passenden Test anhand der Gegebenheiten Deiner Daten auszuwählen.
Abb. 11: Register „Einstellungen“/unabhängige Stichproben
Durch Klicken auf „Ausführen“ erhältst Du dann das Testergebnis:
Abb. 12: Output des Mediantests für unabhängige Stichproben.
SPSS hat den Mann-Whitney-Test als geeignetes Verfahren ausgewählt. Aufgrund der Beobachtungen wird die Nullhypothese, die Gehälter in Frankfurt und Hamburg seien gleich, verworfen. Die berechnete Signifikanz ist mit p=0,011 geringer als die üblicherweise verwendete Irrtumswahrscheinlichkeit α=5%. Im Zweifelsfall greift dir der Statistik-Service unter die Arme.
Mediantest ist der Oberbegriff für eine Reihe von nicht parametrischen Testverfahren zum Vergleich der zentralen Tendenz von Stichproben. Teilst Du SPSS mit, ob die Stichproben abhängig oder unabhängig sind, so wählt das Programm automatisch geeignete Testverfahren aus.
Literatur
Holling, Heinz/Gediga, Günther (2016): Statistik-Testverfahren, 1. Auflage, Göttingen.
Janssen, Jürgen/Laatz, Wilfried (2017): Statistische Datenanalyse mit SPSS. Eine anwendungsorientierte Einführung in das Basissystem und das Modul Exakte Tests, 9. Auflage, Berlin.